Что такое средняя линия треугольника какие свойства вы знаете
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
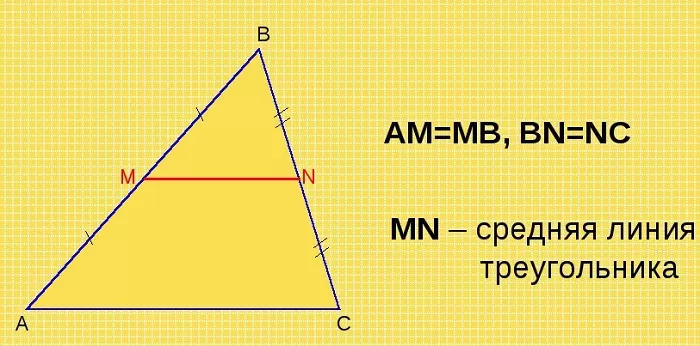
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
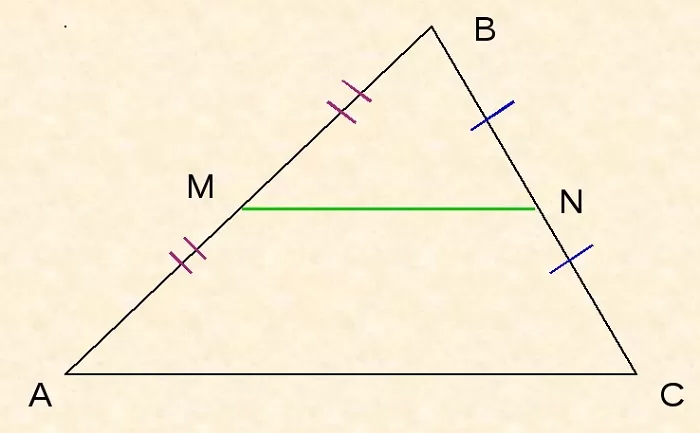
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Первый способ
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
Пусть NP II AB.
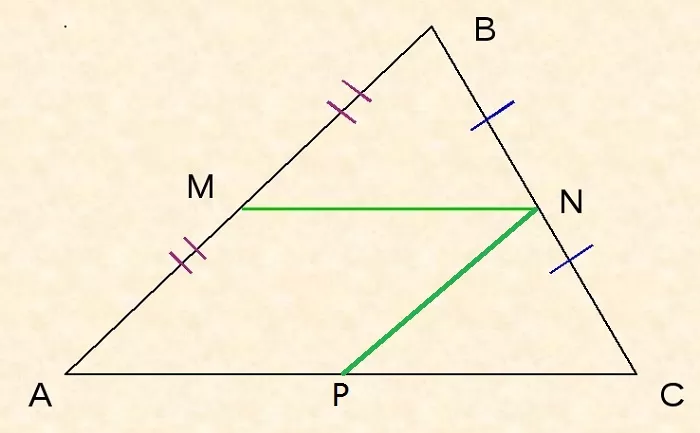
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Доказано.
Второй способ
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
![]()
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
![]()
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Доказано.
Третий способ
Рассматривается сумма векторов
![]()
Поскольку в результате образуется замкнутая ломаная, то
![]()
Отсюда следует, что
![]()
Так как
![]()
то
![]()
![]()
Из последнего равенства следуют условия теоремы.
Доказано.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
Доказательство.

По определению стороны AB и BC делятся пополам, поэтому
![]()
Согласно теореме,
![]()
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
![]()
Доказано.
Следствие №2
Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.
Доказательство.
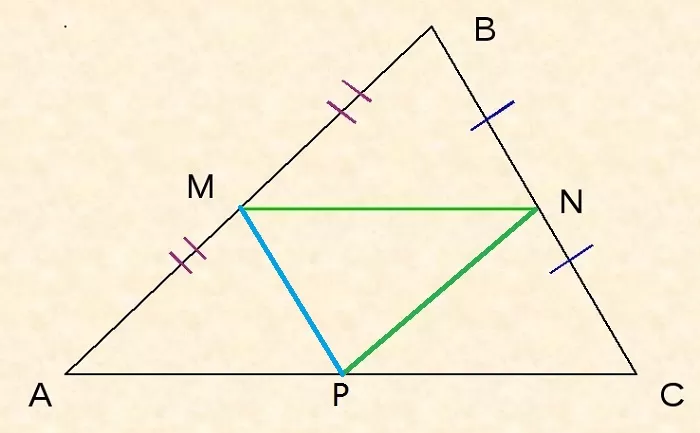
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Доказано.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
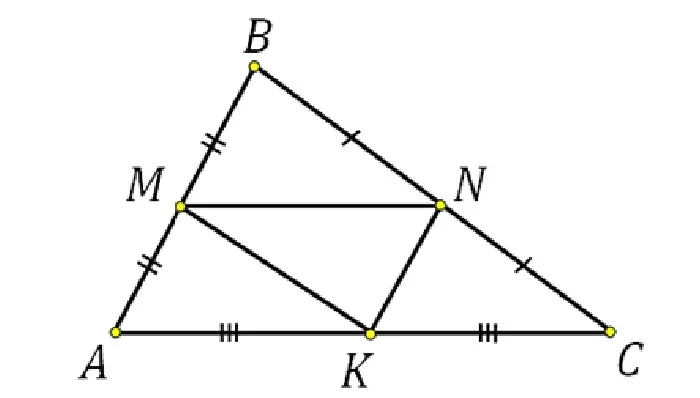
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
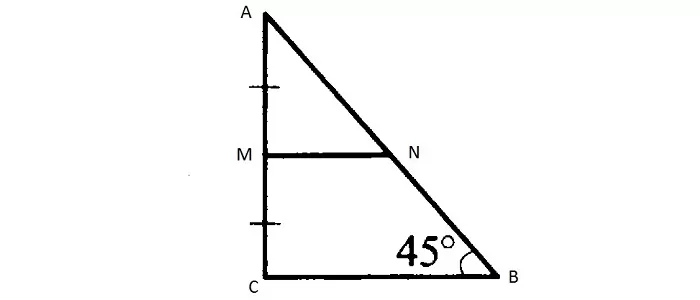
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
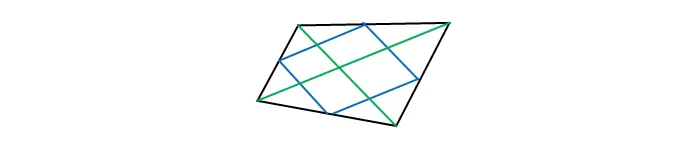
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Решение.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Доказано.
Источник
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Средняя линия треугольника[править | править код]
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника[1].
Свойства[править | править код]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки[править | править код]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника[править | править код]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства[править | править код]
Первая линия соединяет 2 противоположные стороны.
Вторая соединяет 2 другие противоположные стороны.
Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода – четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции[править | править код]
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: , где AD и BC — основания трапеции.
Свойства[править | править код]
- средняя линия параллельна основаниям
- средняя линия равна полусумме оснований
- cредняя линия разбивает фигуру на две трапеции, площади которых соотносятся как [1]
См. также[править | править код]
- Теорема Вариньона (геометрия)
Примечания[править | править код]
Источник
[{Large{text{Подобие треугольников}}}]
Определения
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
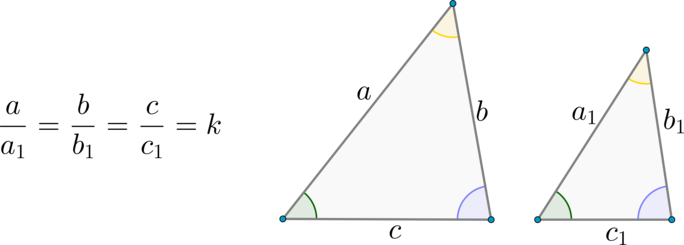
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники (ABC) и (A_1B_1C_1) со сторонами (a,b,c) и (a_1, b_1, c_1) соответственно (см. рисунок выше).
Тогда (P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=kcdot
P_{A_1B_1C_1})
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники (ABC) и (A_1B_1C_1) подобны, причём (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = dfrac{BC}{B_1C_1} = k). Обозначим буквами (S) и (S_1) площади этих треугольников соответственно.
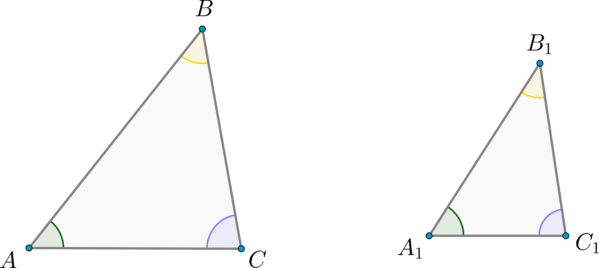
Так как (angle A = angle A_1), то (dfrac{S}{S_1} = dfrac{ABcdot
AC}{A_1B_1cdot A_1C_1}) (по теореме об отношении площадей треугольников, имеющих по равному углу).
Так как (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = k), то (dfrac{S}{S_1} = dfrac{AB}{A_1B_1}cdotdfrac{AC}{A_1C_1} = kcdot k = k^2), что и требовалось доказать.
[{Large{text{Признаки подобия треугольников}}}]
Теорема (первый признак подобия треугольников)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть (ABC) и (A_1B_1C_1) – треугольники такие, что (angle A =
angle A_1), (angle B = angle B_1). Тогда по теореме о сумме углов треугольника (angle C = 180^circ – angle A – angle B = 180^circ
– angle A_1 – angle B_1 = angle C_1), то есть углы треугольника (ABC) соответственно равны углам треугольника (A_1B_1C_1).
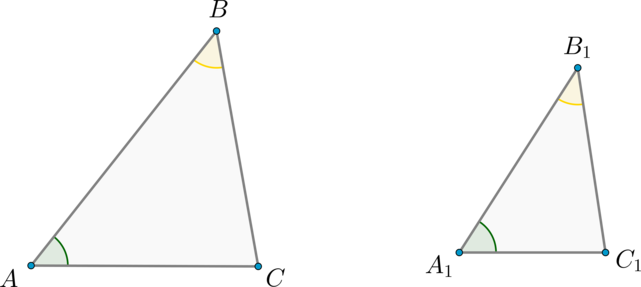
Так как (angle A = angle A_1) и (angle B = angle B_1), то (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1}) и (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot
BC}{A_1B_1cdot B_1C_1}).
Из этих равенств следует, что (dfrac{AC}{A_1C_1} =
dfrac{BC}{B_1C_1}).
Аналогично доказывается, что (dfrac{AC}{A_1C_1} =
dfrac{AB}{A_1B_1}) (используя равенства (angle B = angle B_1), (angle C = angle C_1)).
В итоге, стороны треугольника (ABC) пропорциональны сходственным сторонам треугольника (A_1B_1C_1), что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника (ABC) и (A’B’C’), таких что (dfrac{AB}{A’B’}=dfrac{AC}{A’C’}), (angle BAC = angle A’). Докажем, что треугольники (ABC) и (A’B’C’) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B’).
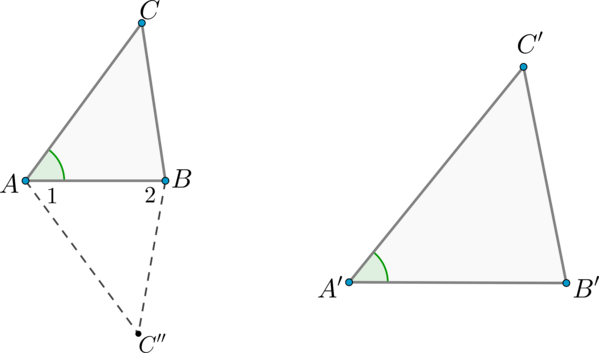
Рассмотрим треугольник (ABC”), у которого (angle 1 = angle A’), (angle 2 = angle B’). Треугольники (ABC”) и (A’B’C’) подобны по первому признаку подобия треугольников, тогда (dfrac{AB}{A’B’} =
dfrac{AC”}{A’C’}).
С другой стороны, по условию (dfrac{AB}{A’B’} = dfrac{AC}{A’C’}). Из последних двух равенств следует, что (AC = AC”).
Треугольники (ABC) и (ABC”) равны по двум сторонам и углу между ними, следовательно, (angle B = angle 2 = angle B’).
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников (ABC) и (A’B’C’) пропорциональны: (dfrac{AB}{A’B’} = dfrac{AC}{A’C’} = dfrac{BC}{B’C’}). Докажем, что треугольники (ABC) и (A’B’C’) подобны.
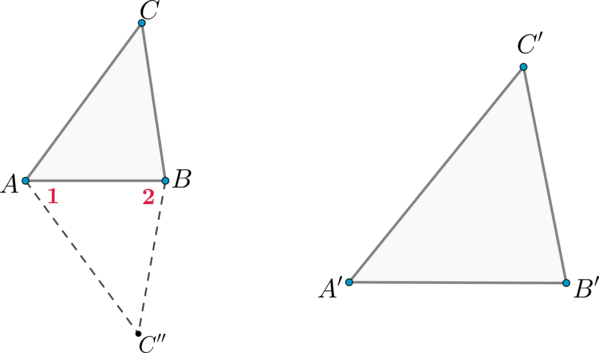
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что (angle BAC = angle A’).
Рассмотрим треугольник (ABC”), у которого (angle 1 = angle A’), (angle 2 = angle B’).
Треугольники (ABC”) и (A’B’C’) подобны по первому признаку подобия треугольников, следовательно, (dfrac{AB}{A’B’} = dfrac{BC”}{B’C’}
= dfrac{C”A}{C’A’}).
Из последней цепочки равенств и условия (dfrac{AB}{A’B’} =
dfrac{AC}{A’C’} = dfrac{BC}{B’C’}) вытекает, что (BC = BC”), (CA
=
C”A).
Треугольники (ABC) и (ABC”) равны по трем сторонам, следовательно, (angle BAC = angle 1 = angle A’).

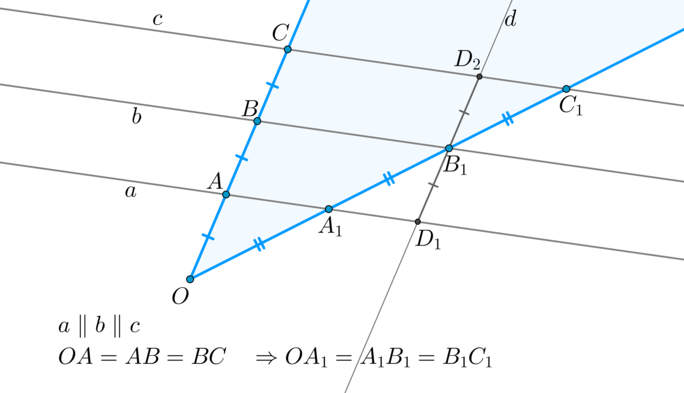
[{Large{text{Теорема Фалеса}}}]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму: Если в (triangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1), то она пересечет сторону (OB_1) также в середине.
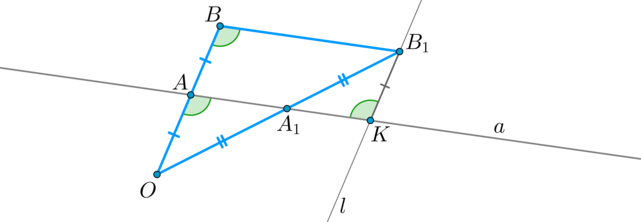
Через точку (B_1) проведем (lparallel OB). Пусть (lcap a=K). Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle
A_1KB_1=angle ABB_1=angle OAA_1); (angle AA_1O=angle KA_1B_1) как вертикальные. Значит, по второму признаку (triangle
OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1). Лемма доказана.

Перейдем к доказательству теоремы. Пусть (OA=AB=BC), (aparallel
bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1).
Таким образом, по данной лемме (OA_1=A_1B_1). Докажем, что (A_1B_1=B_1C_1). Проведем через точку (B_1) прямую (dparallel OC), причем пусть (dcap a=D_1, dcap c=D_2). Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2). Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2) как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1) как накрест лежащие, и, значит, по второму признаку (triangle A_1B_1D_1=triangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1).
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
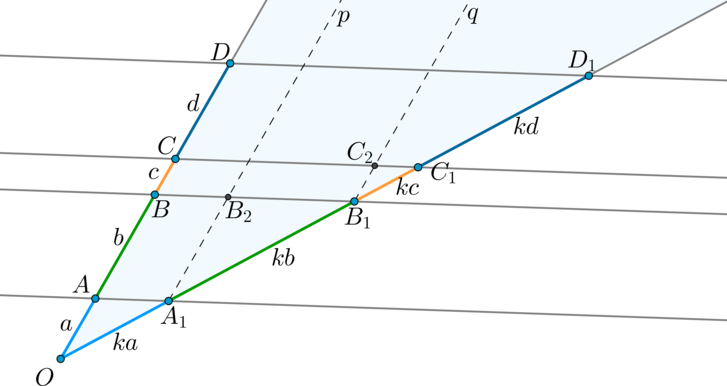
Доказательство
Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d). Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно, где (k) – некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку (A_1) прямую (pparallel OD) ((ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2)). Тогда (triangle OAA_1
sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb).
Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow
triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

[{Large{text{Средняя линия треугольника}}}]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы.
2) Докажем, что (MN=dfrac12 AC).
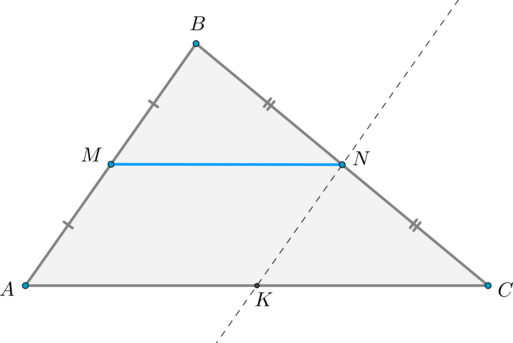
Через точку (N) проведем прямую параллельно (AB). Пусть эта прямая пересекла сторону (AC) в точке (K). Тогда (AMNK) — параллелограмм ((AMparallel NK, MNparallel AK) по предыдущему пункту). Значит, (MN=AK).
Т.к. (NKparallel AB) и (N) – середина (BC), то по теореме Фалеса (K) – середина (AC). Следовательно, (MN=AK=KC=dfrac12 AC).
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12).
Источник
Средние линии треугольника
Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

Рис.1
На рисунке 1 средней линией является отрезок DE.
Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Доказательство. Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Рис.2
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.
Первую часть утверждения 1 мы доказали.
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Рис.3
Поскольку
DE | | FC , DF | | EC ,
то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно, DE = FC .
Поскольку
DE | | AF , AD | | FE ,
то четырёхугольник DEFA – параллелограммчетырёхугольник DEFA – параллелограмм, следовательно, DE = AF .
Но поскольку AF = FC , то отсюда вытекает равенство
что и требуется доказать.
Доказательство утверждения 1 закончено.
Следствие.
- Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
- Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5.

Рис.4
Средняя линия трапеции
Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.
Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).


Рис.5
На рисунке 5 средней линией трапеции является отрезок EF .
Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.


Рис.6
Доказательство. Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
что и требовалось доказать.
Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.


Рис.7
Решение. Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.
Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.


Рис.8
Решение. Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:
Следовательно,
что и требовалось доказать.
Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Рис.9
Доказательство. Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
Заметим также, что треугольник KMC подобен треугольнику NMD . Поэтому
Из этих соотношений получаем:
откуда вытекает, что точки N и L совпадают. Доказательство завершено.
Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.
Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.
Следствие. Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Средние линии четырехугольника. Теорема Вариньона
Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).


Рис.10
На рисунке 10 средние линии – это отрезки EF и GH .
Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

Рис.11
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .
Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.
Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.
Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.
Доказательство. Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.


Рис.12
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

Рис.13
Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.
Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).


Рис.14
Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

Рис.15
Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке O (рис. 16).


Рис.16
В соответствии со свойствами векторов справедливы следующие равенства:
что и требовалось доказать.
Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.
Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.
Средние линии тетраэдра
Тетраэдром называют произвольную треугольную пирамиду (рис.17).

Рис.17
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.
Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

Рис.18
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.
Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Рис.19
Заметим, что отрезок EH является средней линией треугольника ADB , поэтому
Отрезок GF является средней линией треугольника ACB , поэтому
Отсюда вытекает, что отрезки EH и GF равны и параллельны, следовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограмм. Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.
Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.
Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:


Рис.20
Доказательство. По свойствам векторов
что и требовалось доказать.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
