Что такое прямоугольник ромб квадрат какие свойства вы знаете

Предварительные сведения
Для начала разберемся с таким понятием, как параллелограмм.
Определение 1
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Введем теперь, непосредственно, определение параллелограмма.
Определение 2
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой.
Напомним основные свойства параллелограмма.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Рассмотрим далее подробно понятия прямоугольника, ромба и квадрата.
Прямоугольник
Определение 3
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).

Рисунок 1. Прямоугольник
Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$
Рассмотрим два свойства прямоугольника.
Свойство 3: Обе диагонали прямоугольника равны между собой.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.
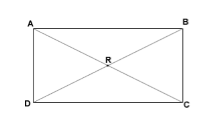
Рисунок 2.
Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем
Так как $angle B=angle A={90}^0$, а $AB$ – общая сторона, то по I признаку равенства треугольников, $triangle ABD=triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $angle DRC=angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $triangle DRC=triangle ARB$. Значит, $angle RDC=angle RCD=angle RAB={rm }angle RBA$.
Так как $angle DRA=angle CRB$, как вертикальные, то по I признаку равенства треугольников $triangle DRA=triangle CRB$. Значит, $angle RDA=angle RAD=angle RCB={rm }angle RBC$.
Следовательно, $angle A=angle B=angle C=angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Ромб
Определение 4
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 3).
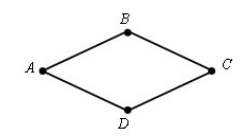
Рисунок 3. Ромб
Рассмотрим свойство ромба.
Свойство 5: Диагонали ромба являются биссектрисами его углов и перпендикулярны друг другу.
Доказательство.
Пусть нам дан ромб $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $E$ (рис. 4).
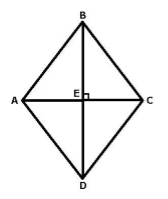
Рисунок 4.
Так как ромб является прямоугольником с равными сторонами, то
Следовательно, по третьему признаку равенства треугольников,
Это доказывает, что диагонали являются биссектрисами углов ромба.
Так как $AB=AD$, то треугольник $ABD$ равнобедренный, а так как $AE$ – медиана треугольника $ABD$, то $AC$ перпендикулярно $BD$.
Свойство доказано.
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).
Рисунок 5. Квадрат
Очевидно, что квадрат — частный случай ромба. Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.
Пример задачи
Пример 1
Найти периметр квадрата, диагональ которого равняется $10$.
Решение.
Обозначим сторону квадрата через $a$. Тогда, по теореме Пифагора
[a^2+a^2=100] [{2a}^2=100] [a^2=50] [a=5sqrt{2}] [P=4a=20sqrt{2}]
Ответ: $20sqrt{2}$.
Источник
Прямоугольник – параллелограмм, у которого все углы прямые.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника. Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны.
- Каждый угол прямоугольника равен 90°.
- Значит, противоположные углы равны и сумма углов, прилежащих к одной стороне, равна 180°.
- Диагонали прямоугольника точкой пересечения делятся пополам.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Накрест лежащие углы при диагонали равны.
- Диагонали прямоугольника равны.
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
- Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
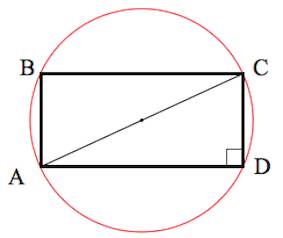
Признаки прямоугольника
- Если три угла четырехугольника прямые, то этот четырехугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны и для квадрата.
- Все четыре стороны квадрата имеют одинаковую длину, то есть они равны.
- Противоположные стороны квадрата параллельны.
- Сумма углов квадрата равна 360°.
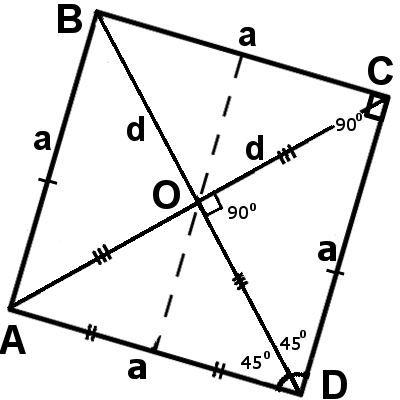
- Диагонали квадрата имеют одинаковые длины.
- Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные, и прямоугольные.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Формулы определения длины диагонали квадрата:
(d=asqrt{2}; d=sqrt{2S}; d=2R; d=2rsqrt{2}).
Ромбом называется параллелограмм, у которого все стороны равны. Если у ромба все углы прямые, тогда он называется квадратом.
Свойства ромба
- Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
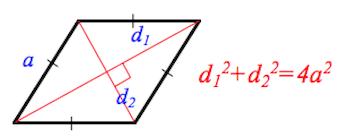
- Диагонали перпендикулярны.
- Диагонали являются биссектрисами его углов.
- Центром вписанной в ромб окружности будет точка пересечения его диагоналей.
Признаки ромба
- Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.
- Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.
Формулы определения длины стороны ромба:
(a=frac{S}{h_a}; a=sqrt{frac{S}{sinalpha}}; a=frac{S}{2r}; a=frac{sqrt{d_1^2+d_2^2}}{2}).
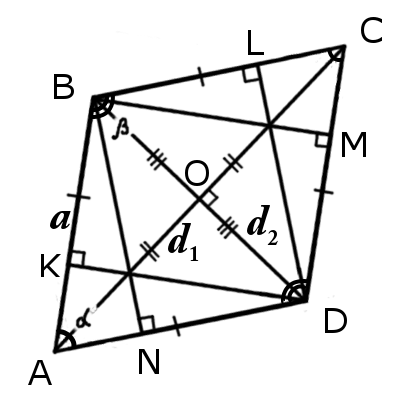
Формулы определения длины диагонали ромба:
(d_1=asqrt{2-2cosbeta}; d_2=asqrt{2+2cosbeta}; d_1=sqrt{4a^2-d_2^2}; d_2=sqrt{4a^2-d_1^2}).
Диагональ ромба равна его стороне. Найдите меньший угол ромба.
В параллелограмме (ABCD) сторона (AB=7, AD=3,sinA=frac67). Найдите большую высоту параллелограмма.
Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10.
Диагональ квадрата равна (2sqrt{8}) см. Найдите сторону квадрата.
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Числовое значение площади прямоугольника принадлежит промежутку
Источник
Видеоурок 1: Прямоугольник, ромб и квадрат. Часть 1
Видеоурок 2: Прямоугольник, ромб и квадрат. Часть 2
Лекция: Параллелограмм, прямоугольник, ромб, квадрат
Четырехугольники
Один подраздел многоугольников мы изучили в прошлом вопросе, сейчас же перейдем к изучению четырехугольников – это многоугольники, у которых 4 стороны, 4 вершины, 4 угла.
В школьном курсе геометрии изучают несколько основных типов четырехугольников – это параллелограмм, прямоугольник, ромб, квадрат и трапецию. В этом же вопросы мы рассмотрим все, кроме трапеции, поскольку все первые 4 типа многоугольников имеют некоторые похожие черты – у них противолежащая пара сторон параллельна.
Отличительная особенность всех четырехугольников – это то, что сумма всех углом равна 360 градусов.
Ну давайте начнем характеризовать все четырехугольники, имеющиеся в теме.
Параллелограмм
Исходя из названия, можно судить, что у данного четырехугольника что-то параллельное. Это совершенно верно, параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.

Все четырехугольники характеризуются своими свойствами, поэтому давайте ознакомимся со свойствами параллелограмма:
Параллельные стороны параллелограмма попарно равны между собой

Противолежащие углы параллелограмма также равны

Диагонали параллелограмма пересекаются в точке, которая делит из пополам

Если у четырехугольника присутствуют перечисленные свойства, то он является параллелограммом:
- Какой – то Один признак выполнен
- Все свойства параллелограмма можно использовать
Для любого параллелограмма справедлива следующая формула, по которой ясно, что сумма квадратов сторон диагоналей равна сумме квадратов всех сторон:
Данное свойство вытекает из теоремы Пифагора для двух прямоугольных треугольников.
Любую сторону можно найти по известным величинам диагоналей и углов между ними:

Найти стороны параллелограмма можно не только через диагонали, но и через высоты и площади:

Одними из наиболее важных формул являются формулы для нахождения диагоналей найти их можно по известным сторонам и углу между ними:

Но на самом деле самыми важными формулами являются формулы для нахождения площадей:

Квадрат
Правильный четырехугольник – это квадрат. Как известно, у всех правильных фигур равны стороны и равны углы. Квадрат можно назвать частным случаем параллелограмма, поскольку все свойства и признаки параллелограмма видны и у квадрата.Свойства квадрата:
- Все стороны равны.
- Все углы равны 90 градусам.
- Диагонали квадрата равны и пересекаются под прямым углом, а точка их пересечения делит их пополам.

Отличительной особенностью диагонали квадрата является то, что она есть гипотенузой прямоугольного треугольника с катетами, равными сторонам квадрата, а гипотенузой равной диагонали. Именно поэтому из теоремы Пифагора диагональ квадрата всегда в раз больше его стороны.

Так как у квадрата все стороны равны, то найти периметр и площадь этой фигуры не составляет ни малейшего труда:


Прямоугольник
Эта фигура характеризуется тем, что все её углы прямые, то есть по 90 градусов.
Свойства прямоугольника:
У прямоугольника все противолежащие стороны параллельны и равны между собой.
Все углы прямые.
Точка пересечения диагоналей делит их на равные части.

Квадрат диагонали прямоугольника равен сумме квадратов его сторон:
Как можно было понять, данная формула была выведена из теоремы Пифагора, поскольку в основе прямоугольника лежат 2 прямоугольных треугольника.
Формулы нахождения сторон по известным величинам диагоналей, а также площадей:
Формулы сторон прямоугольника

Формулы периметра прямоугольника

Формулы площадей

Ромб
И наконец-то мы подошли к последнему из параллелограммов, который называется ромбом.
У ромба, как и у квадрата, все стороны равно, но, как и у любого параллелограмма, его стороны попарно параллельны.
Отличительной особенностью ромба считается то, что его диагонали, пересекаясь под прямым углом, делятся пополам.
Не имеет смысла перечислять все свойства ромба, поскольку они аналогичны свойствам параллелограмма, а так же квадрата.
У ромба так же существует связь между длинами диагоналей и его сторон. Поскольку в основании ромба лежат 4 прямоугольных треугольника, то можно было вывести формулу связи диагоналей и сторон через теорему Пифагора:
Формулы для сторон ромба

Формулы площадей ромба

Источник
Урок № 9
Тема: Прямоугольник, ромб, квадрат и их свойства
Цель урока:
Обучающие –познакомить с определениями прямоугольника, ромба, квадрата, а также свойствами каждого из них; научить указывать их общие свойства и различия;
Развивающие –развитие любознательности, логического мышления, наблюдательности;
Воспитывающие –воспитание познавательного интереса к предмету.
Тип урока: формирование новых знаний, умений.
Ход урока
1.Орг.момент
Перед изучением нового материала проводится входной контроль умений и навыков учащихся для определения уровня готовности к восприятию новой темы.
2.Повторение теоретического материала
-Определение параллелограмма.
-Свойства параллелограмма.
-Свойство медианы равнобедренного треугольника, проведенной к его основанию.
-Устно по рисунку на доске доказать, что ЕК = АМ, если , ЕМ = КА.
3.Актуализация знаний
Среди параллелограммов есть фигуры, имеющие особые названия. С этими фигурами, их свойствами вам предстоит сегодня познакомиться.
ПРЯМОУГОЛЬНИК. С этой фигурой ты знаком уже давно. Попробуй сформулировать его определение.
Прямоугольником называется параллелограмм, у которого…
Так как прямоугольник по определению является параллелограммом, то для него справедливы и все свойства параллелограмма. Попробуй их сформулировать и запиши в тетрадь.
Но у прямоугольника есть и свое особое свойство, которое тебе предстоит доказать.
ТЕОРЕМА. Диагонали прямоугольника равны.
Дано:
ABCD – прямоугольник
Доказать: AC = BD
Чтобы доказать равенство отрезков AC и BD , надо доказать равенство прямоугольных треугольников ACD и DBA (по двум катетам).
Докажем обратное утверждение (признак прямоугольника): Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Дано:
ABCD – параллелограмм
AC = BD
Доказать:
ABCD – прямоугольник
Доказательство:
1. Рассмотрим и
AD – общая сторона
AC = BD по условию
AB = CD по свойству параллелограмма
Следовательно, = по …
Значит,
2. ABCD – параллелограмм, следовательно, его противолежащие углы
равны, т.е. , но параллелограмм – это выпуклый четырехугольник, значит сумма его углов равна 360о.
Вывод: все углы данного параллелограмма по 90о, следовательно, он является прямоугольником.
Реши задачу (устно)
В прямоугольнике ABCD диагональ АС образует со стороной AD угол, равный 40о. Найти градусную меру угла ACD
РОМБ.
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Как на рисунке показать, что
данный параллелограмм – ромб?
Так как ромб – параллелограмм,
То он обладает всеми его
свойствами.
Рассмотри особое свойство ромба.
ТЕОРЕМА. Диагонали ромба взаимно перпендикулярны и делят углы ромба пополам.
Дано: АВСD – ромб
Доказать:
1) АС BD;
2)
Доказательство:
АВСD – ромб, следовательно АВ = ВС, значит АВС – равнобедренный с основанием АС.
Диагонали ромба точкой пересечения делятся пополам, следовательно, точка О – середина АС, т.е. ВО – медиана АВС.
Вывод: ВО АС; ,т.к. в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Реши задачи (устно)
Периметр ромба – 56 см. Найти длину стороны ромба.
В ромбе АВСD угол ВАD равен 50о. Найти углы треугольника ABD.
КВАДРАТ. Термин “квадрат” происходит от латинского quadratus, что в переводе означает четырехугольник. Квадрат был первым четырехугольником, который рассматривался в геометрии.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Но мы можем дать и другие определения квадрата.
Квадрат – это ромб, у которого…
Квадрат – это параллелограмм, у которого…
Отсюда следует, что квадрат обладает всеми свойствами параллелограмма, ромба и прямоугольника.
Все углы квадрата равны.
Диагонали квадрата равны
Диагонали квадрата точкой пересечения делятся пополам.
Диагонали квадрата взаимно перпендикулярны и делят его углы пополам.
Реши задачи (устно)
В квадрате АВСD проведена диагональ АС. Определи
вид треугольника АВС и углы треугольника АВС.
Сейчас тебе предстоит оценить свою работу. Для этого вернись к УЭ – 0 и подумай, достиг ли ты цели нашего урока. Если да, то переходи к следующему этапу работы – проверке знаний.
Вопросы для контроля.
Перечисли четырехугольники, обладающие следующими свойствами:
Диагонали точкой пересечения делятся пополам.
Диагонали равны.
Углы, прилежащие к одной стороне, равны.
Диагонали делят углы пополам.
Диагонали взаимно перпендикулярны.
Противолежащие углы равны.
Все углы равны.
Диагонали равны и взаимно перпендикулярны.
Домашнее задание: §
Источник
| 1. | Периметр прямоугольника Сложность: | 2 |
| 2. | Cторона квадрата Сложность: | 1 |
| 3. | Параллельные прямые Сложность: | 4 |
| 4. | Элементы квадрата Сложность: | 3 |
| 5. | Периметр ромба Сложность: | 1 |
| 6. | Вопросы о свойствах прямоугольника Сложность: | 1 |
| 7. | Вопросы о свойствах и признаках прямоугольника Сложность: | 2 |
| 8. | Стороны прямоугольника, дано их отношение и Р Сложность: | 2 |
| 9. | Диагонали ромба Сложность: | 1 |
| 10. | Углы ромба Сложность: | 2 |
| 11. | Периметр прямоугольника Сложность: | 3 |
| 12. | Вопросы о свойствах и признаках квадрата Сложность: | 2 |
| 13. | Стороны прямоугольника, дано их соотношение и P Сложность: | 3 |
| 14. | Углы между диагональю и сторонами прямоугольника Сложность: | 3 |
| 15. | Меньшая диагональ ромба Сложность: | 3 |
| 16. | Угол ромба, дан угол между диагональю и стороной ромба Сложность: | 3 |
| 17. | Острый угол ромба, дана разность углов Сложность: | 3 |
| 18. | Углы ромба (уравнение) Сложность: | 3 |
| 19. | Угол ромба, дан угол между высотой и стороной ромба Сложность: | 3 |
| 20. | Угол ромба, если меньшая диагональ равна стороне Сложность: | 3 |
| 21. | Элементы треугольника, образованного диагональю и стороной ромба Сложность: | 3 |
| 22. | Угол между диагоналями прямоугольника Сложность: | 3 |
| 23. | Квадрат, вписанный в прямоугольный треугольник Сложность: | 1 |
| 24. | Доказательство с использованием свойств квадрата Сложность: | 1 |
Источник
