Что такое прямоугольник ромб квадрат какие свойства
Предварительные сведения
Для начала разберемся с таким понятием, как параллелограмм.
Определение 1
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Введем теперь, непосредственно, определение параллелограмма.
Определение 2
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой.
Напомним основные свойства параллелограмма.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Рассмотрим далее подробно понятия прямоугольника, ромба и квадрата.
Прямоугольник
Определение 3
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).

Рисунок 1. Прямоугольник
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$
Рассмотрим два свойства прямоугольника.
Свойство 3: Обе диагонали прямоугольника равны между собой.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.
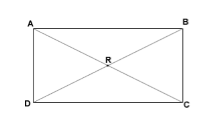
Рисунок 2.
Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем
Так как $angle B=angle A={90}^0$, а $AB$ – общая сторона, то по I признаку равенства треугольников, $triangle ABD=triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $angle DRC=angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $triangle DRC=triangle ARB$. Значит, $angle RDC=angle RCD=angle RAB={rm }angle RBA$.
Так как $angle DRA=angle CRB$, как вертикальные, то по I признаку равенства треугольников $triangle DRA=triangle CRB$. Значит, $angle RDA=angle RAD=angle RCB={rm }angle RBC$.
Следовательно, $angle A=angle B=angle C=angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Ромб
Определение 4
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 3).
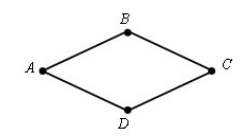
Рисунок 3. Ромб
Рассмотрим свойство ромба.
Свойство 5: Диагонали ромба являются биссектрисами его углов и перпендикулярны друг другу.
Доказательство.
Пусть нам дан ромб $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $E$ (рис. 4).
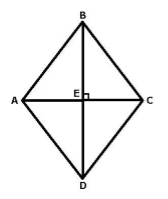
Рисунок 4.
Так как ромб является прямоугольником с равными сторонами, то
Следовательно, по третьему признаку равенства треугольников,
Это доказывает, что диагонали являются биссектрисами углов ромба.
Так как $AB=AD$, то треугольник $ABD$ равнобедренный, а так как $AE$ – медиана треугольника $ABD$, то $AC$ перпендикулярно $BD$.
Свойство доказано.
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).

Рисунок 5. Квадрат
Очевидно, что квадрат — частный случай ромба. Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.
Пример задачи
Пример 1
Найти периметр квадрата, диагональ которого равняется $10$.
Решение.
Обозначим сторону квадрата через $a$. Тогда, по теореме Пифагора
[a^2+a^2=100] [{2a}^2=100] [a^2=50] [a=5sqrt{2}] [P=4a=20sqrt{2}]
Ответ: $20sqrt{2}$.
Источник
Урок № 9
Тема: Прямоугольник, ромб, квадрат и их свойства
Цель урока:
Обучающие –познакомить с определениями прямоугольника, ромба, квадрата, а также свойствами каждого из них; научить указывать их общие свойства и различия;
Развивающие –развитие любознательности, логического мышления, наблюдательности;
Воспитывающие –воспитание познавательного интереса к предмету.
Тип урока: формирование новых знаний, умений.
Ход урока
1.Орг.момент
Перед изучением нового материала проводится входной контроль умений и навыков учащихся для определения уровня готовности к восприятию новой темы.
2.Повторение теоретического материала
-Определение параллелограмма.
-Свойства параллелограмма.
-Свойство медианы равнобедренного треугольника, проведенной к его основанию.
-Устно по рисунку на доске доказать, что ЕК = АМ, если , ЕМ = КА.
3.Актуализация знаний
Среди параллелограммов есть фигуры, имеющие особые названия. С этими фигурами, их свойствами вам предстоит сегодня познакомиться.
ПРЯМОУГОЛЬНИК. С этой фигурой ты знаком уже давно. Попробуй сформулировать его определение.
Прямоугольником называется параллелограмм, у которого…
Так как прямоугольник по определению является параллелограммом, то для него справедливы и все свойства параллелограмма. Попробуй их сформулировать и запиши в тетрадь.
Но у прямоугольника есть и свое особое свойство, которое тебе предстоит доказать.
ТЕОРЕМА. Диагонали прямоугольника равны.
Дано:
ABCD – прямоугольник
Доказать: AC = BD
Чтобы доказать равенство отрезков AC и BD , надо доказать равенство прямоугольных треугольников ACD и DBA (по двум катетам).
Докажем обратное утверждение (признак прямоугольника): Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Дано:
ABCD – параллелограмм
AC = BD
Доказать:
ABCD – прямоугольник
Доказательство:
1. Рассмотрим и
AD – общая сторона
AC = BD по условию
AB = CD по свойству параллелограмма
Следовательно, = по …
Значит,
2. ABCD – параллелограмм, следовательно, его противолежащие углы
равны, т.е. , но параллелограмм – это выпуклый четырехугольник, значит сумма его углов равна 360о.
Вывод: все углы данного параллелограмма по 90о, следовательно, он является прямоугольником.
Реши задачу (устно)
В прямоугольнике ABCD диагональ АС образует со стороной AD угол, равный 40о. Найти градусную меру угла ACD
РОМБ.
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Как на рисунке показать, что
данный параллелограмм – ромб?
Так как ромб – параллелограмм,
То он обладает всеми его
свойствами.
Рассмотри особое свойство ромба.
ТЕОРЕМА. Диагонали ромба взаимно перпендикулярны и делят углы ромба пополам.
Дано: АВСD – ромб
Доказать:
1) АС BD;
2)
Доказательство:
АВСD – ромб, следовательно АВ = ВС, значит АВС – равнобедренный с основанием АС.
Диагонали ромба точкой пересечения делятся пополам, следовательно, точка О – середина АС, т.е. ВО – медиана АВС.
Вывод: ВО АС; ,т.к. в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Реши задачи (устно)
Периметр ромба – 56 см. Найти длину стороны ромба.
В ромбе АВСD угол ВАD равен 50о. Найти углы треугольника ABD.
КВАДРАТ. Термин “квадрат” происходит от латинского quadratus, что в переводе означает четырехугольник. Квадрат был первым четырехугольником, который рассматривался в геометрии.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Но мы можем дать и другие определения квадрата.
Квадрат – это ромб, у которого…
Квадрат – это параллелограмм, у которого…
Отсюда следует, что квадрат обладает всеми свойствами параллелограмма, ромба и прямоугольника.
Все углы квадрата равны.
Диагонали квадрата равны
Диагонали квадрата точкой пересечения делятся пополам.
Диагонали квадрата взаимно перпендикулярны и делят его углы пополам.
Реши задачи (устно)
В квадрате АВСD проведена диагональ АС. Определи
вид треугольника АВС и углы треугольника АВС.
Сейчас тебе предстоит оценить свою работу. Для этого вернись к УЭ – 0 и подумай, достиг ли ты цели нашего урока. Если да, то переходи к следующему этапу работы – проверке знаний.
Вопросы для контроля.
Перечисли четырехугольники, обладающие следующими свойствами:
Диагонали точкой пересечения делятся пополам.
Диагонали равны.
Углы, прилежащие к одной стороне, равны.
Диагонали делят углы пополам.
Диагонали взаимно перпендикулярны.
Противолежащие углы равны.
Все углы равны.
Диагонали равны и взаимно перпендикулярны.
Домашнее задание: §
Источник
Прямоугольник – параллелограмм, у которого все углы прямые.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника. Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны.
- Каждый угол прямоугольника равен 90°.
- Значит, противоположные углы равны и сумма углов, прилежащих к одной стороне, равна 180°.
- Диагонали прямоугольника точкой пересечения делятся пополам.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Накрест лежащие углы при диагонали равны.
- Диагонали прямоугольника равны.
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
- Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
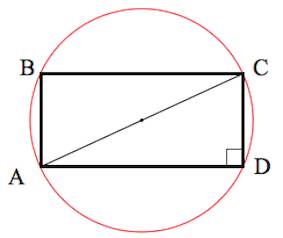
Признаки прямоугольника
- Если три угла четырехугольника прямые, то этот четырехугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны и для квадрата.
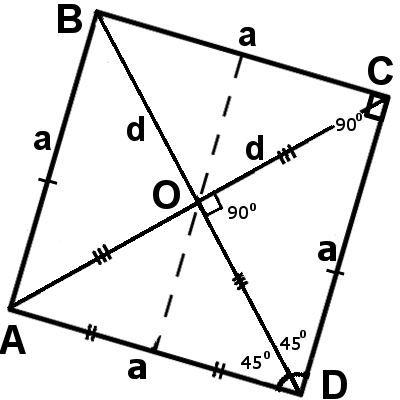
- Все четыре стороны квадрата имеют одинаковую длину, то есть они равны.
- Противоположные стороны квадрата параллельны.
- Сумма углов квадрата равна 360°.
- Диагонали квадрата имеют одинаковые длины.
- Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные, и прямоугольные.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Формулы определения длины диагонали квадрата:
(d=asqrt{2}; d=sqrt{2S}; d=2R; d=2rsqrt{2}).
Ромбом называется параллелограмм, у которого все стороны равны. Если у ромба все углы прямые, тогда он называется квадратом.
Свойства ромба
- Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
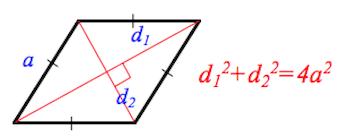
- Диагонали перпендикулярны.
- Диагонали являются биссектрисами его углов.
- Центром вписанной в ромб окружности будет точка пересечения его диагоналей.
Признаки ромба
- Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.
- Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.
Формулы определения длины стороны ромба:
(a=frac{S}{h_a}; a=sqrt{frac{S}{sinalpha}}; a=frac{S}{2r}; a=frac{sqrt{d_1^2+d_2^2}}{2}).
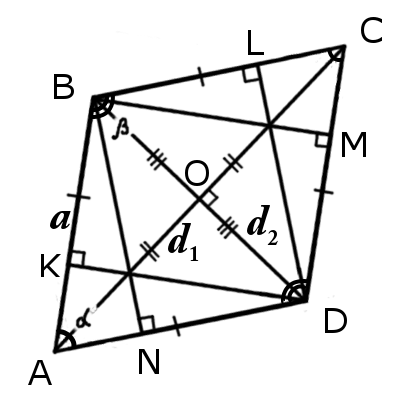
Формулы определения длины диагонали ромба:
(d_1=asqrt{2-2cosbeta}; d_2=asqrt{2+2cosbeta}; d_1=sqrt{4a^2-d_2^2}; d_2=sqrt{4a^2-d_1^2}).
Диагональ ромба равна его стороне. Найдите меньший угол ромба.
В параллелограмме (ABCD) сторона (AB=7, AD=3,sinA=frac67). Найдите большую высоту параллелограмма.
Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10.
Диагональ квадрата равна (2sqrt{8}) см. Найдите сторону квадрата.
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Числовое значение площади прямоугольника принадлежит промежутку
Источник
«Прямоугольник. Ромб. Квадрат»
Номинация: Современные образовательные технологии.
Технология: личностно ориентированное обучение.
Ст. Озерки 2014
Тема урока Прямоугольник. Ромб. Квадрат.
Характеристика класса: В классе обучается 14 человек. Не каждый учащийся способен работать активно, но с заданиями справляется почти каждый. Ребята дисциплинированы, стараются друг другу помогать. В классе сильно развита взаимопомощь.
Цель урока: ознакомление учащихся с понятиями прямоугольника, ромба, квадрата.
Комбинированный урок – сочетает в себе повторение и обобщение знаний, полученных ранее, изучение нового материала и первичное закрепление полученных знаний при доказательстве теорем и решении задач.
Средства, обеспечивающий учебный процесс на уроке: учебник, тетрадь, раздаточный материал, сигнальные карточки.
1. Организационный момент
Цель этапа: включение обучающихся в деятельность
Задачи: Создание положительного эмоционального настроя учащихся к работе на уроке
Деятельность учащихся
Деятельность учителя
Формируемые УУД
Проверяют свою готовность к уроку.
Называют отсутствующих.
Осознание целей урока и настрой на рабочий лад.
Здравствуйте. Садитесь. Проверьте, все ли готовы к уроку? Дежурные, назовите отсутствующих.
Итак, начнем сегодняшний урок.
Ребята, на прошлых уроках мы подробно познакомились с параллелограммом. Однако, существуют и другие виды четырехугольников. Сегодня на уроке вы будем исследовать их свойства.
Саморегуляция (Р).
Планирование учебного сотрудничества с учителем и сверстниками (К).
2. Целеполагание.
Цель: включение учащихся в обсуждение проблемных вопросов и определения темы урока
Задачи: Обеспечение мотивационной готовности учащихся, активизация их УПД
Ставят цели урока.
-повторить параллелограмм и его свойства,
-узнать определения прямоугольника, ромба, квадрата,
-выявить их свойства.
Посмотрите на тему урока, и скажите, каких целей мы должны сегодня достигнуть?
Умение выражать мысли (К).
Планирование, целеполагание (Р).
Смыслообразование – (Л)
Самостоятельное выделение и формулирование познавательной цели (П)
3. Опрос учащихся по заданному на дом материалу
Цель: повторение изученного материала, необходимого для «открытия нового знания»
Задачи: Проверка полноты знаний, сформированности умений, определение «слабых» моментов в усвоении знаний и умений.
Деятельность учащихся
Деятельность учителя
Формируемые УУД
Правильные ответы детей:
1)Параллелограмм. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
2) Противоположные стороны и углы равны; сумма углов, прилежащих к одной стороне равна 180°; диагонали точкой пересечения делятся пополам.
3) если противоположные стороны попарно параллельны; если две стороны равны и параллельны.
Ответы:
- 3,4,5,6
- Потому что либо одна только одна пара сторон параллельна, либо ни одной
- 3 – все стороны равны, 5 – все углы прямые, 4 – все стороны равны, все углы прямые
3 вида: прямоугольник (все углы прямые), ромб (все стороны равны), квадрат (все углы прямые и стороны равны.
Ответьте на вопросы:
1) Какие виды четырехугольников вы уже знаете? Дайте определение.
2) Какими свойствами обладает параллелограмм?
3) По каким признакам можно доказать, что четырехугольник – параллелограмм?
Обратите внимание на рисунки, висящие на доске. (Приложение №1)
Вопросы:
- Назовите номера тех многоугольников, которые являются параллелограммом.
- Почему другие многоугольники не являются параллелограммом?
- Чем данные параллелограммы отличаются друг от друга?
Сколько можно выделить видов параллелограммов?
Умение выражать мысли (К).
4. Изучение нового учебного материала.
Цель: обеспечение восприятия, осмысления и первичного закрепления учащимися основных понятий о прямоугольнике, ромбе, квадрате
Задачи: Создание условий для формирования понятий прямоугольника, квадрата, ромба
Деятельность учащихся
Деятельность учителя
Формируемые УУД
Ответ: все углы прямые.
Ответ: один прямой угол
Ответ: все углы прямые
Ответ: 1) противоположные стороны равны
2) противоположные углы равны
3) диагонали точкой пересечения делятся пополам.
Ответ: диагонали у прямоугольника равны
Ответ: диагонали равны.
Учащиеся делают чертеж и необходимые краткие записи определения, свойства и признака прямоугольника в тетрадях:
Определение. Прямоугольник – параллелограмм, у которого все углы прямые
∠ A = ∠C =∠B =∠D = 90
Свойства:
1)AВ = CВ, BС = АD;
2) AB ⏐⏐ CD, BC ⏐⏐ AD
3) BO=DO, AO=OD
Дано: ABCD – пар-мм, BD = AC
Док-во:
1.Треугольники ABC и BAD равны (по трем сторонам): AB – общая сторона, AC = BD,
BC = AD
2. ∠B = ∠A, следует из 1 пункта
3. Но ∠B + ∠A = 180°, значит ∠B = ∠A = 90° , т.е. ABCD – прямоугольник.
Ответ: все стороны равны.
Ответ: равенство смежных сторон.
Ответ: все стороны равны.
Ответ: диагонали ромба перпендикулярны и являются биссектрисами его углов.
Ответ: все стороны равны
Учащиеся делают чертеж и необходимые краткие записи определения, свойств и признаков ромба в тетрадях.
Определение:
1.Ромб – параллелограмм, у которого все стороны равны.
AB=BC=AC=AD
Свойства ромба:
1)∠A = ∠C, ∠B = ∠D;
2) AB ⏐⏐ CD, BC ⏐⏐ AD
3) ∠A + ∠B = 180°, ∠C + ∠D = 180°
4) BO=DO, AO=OD
Дано: ABCD – пар-м, BD ⊥ AC
Док-во:
1.Прямоугольные треугольники AOB и AOD равны (по двум катетам): BO=OD, AO – общий катет.
2. AB = AD, следует из 1 пункта
3. AB=BC=CD=AD, т.е. ABCD – ромб.
Ответ: 1) все углы прямые;
2) все стороны равны
Ответ: квадрат обладает свойствами и параллелограмма, и ромба и прямоугольника.
Перед вами первый вид параллелограмма – прямоугольник. Давайте дадим ему определение. Закончите предложение: прямоугольник – параллелограмм, у которого…
А как еще можно определить прямоугольник? Сколько достаточно иметь прямых углов параллелограмму, чтобы он стал прямоугольником?
А можно ли дать определение прямоугольника через четырехугольник? Если да, то продолжите предложение: прямоугольник – четырехугольник, у которого…
Итак, прямоугольник – это параллелограмм, значит какими уже известными вам свойствами, он обладает?
А что вы можете сказать о диагоналях прямоугольника?
Ребята, а теперь подумайте и ответьте на вопрос. А каков признак прямоугольника? Закончите предложение: параллелограмм – прямоугольник, если…
Теорема: Если в параллелограмме диагонали равны, то он является прямоугольником.
Особые свойства прямоугольника:
1)все углы прямые;
2)диагонали прямоугольника равны
Перед вами второй вид параллелограмма – ромб. Давайте дадим ему определение. Закончите предложение: ромб – параллелограмм, у которого…
А как еще можно определить ромб? Равенство, каких сторон параллелограмма достаточно, чтобы он стал ромбом?
А можно ли дать определение ромба через четырехугольник? Если да, то продолжите предложение: ромб – четырехугольник, у которого…
А теперь давайте сформулируем свойства ромба, кроме тех которые он уже имеет, являясь параллелограммом. Новые свойства касаются диагоналей ромба. Что вы скажите про треугольник АВD? Чем является в этом треугольнике отрезок АО? Каковы же свойства диагоналей ромба?
Ребята, а как вы считаете, доказанные выше свойства могут быть и признаками ромба? Закончите предложение: параллелограмм – ромб, если…
Признак ромба:
Если в параллелограмме диагонали перпендикулярны, то он является ромбом.
Вывод:
1) все стороны ромба равны;
2) диагонали ромба перпендикулярны;
3) диагонали ромба являются биссектрисами углов.
И наконец, самым идеальным видом параллелограмма является квадрат. Посмотрите внимательно на квадрат и давайте дадим ему определение. Закончите предложения: 1) квадрат – ромб, у которого…;
2)квадрат – прямоугольник, у которого …
Ребята, а как вы думаете, почему я назвала квадрат идеальным видом параллелограмма?
Контроль, коррекция, самооценка действий
5. Закрепление учебного материала
Цель: проговаривание и закрепление нового знания; выявить пробелы первичного осмысления изученного материала, неверные представления учащихся; провести коррекцию
Задачи: Создание условий для развития умений учащихся применять полученные знания в новых ситуациях.
Деятельность учащихся
Деятельность учителя
Формируемые УУД
Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны:
AB=BC=CD=AD, ∠ A = ∠C =∠B =∠D = 90°
Свойство квадрата: AB ⏐⏐ CD, BC ⏐⏐ AD, BO=DO, AO=OD
Признаки квадрата: Если в параллелограмме все стороны равны и все углы прямые, то такой параллелограмм является квадратом
Особые свойства квадрата: диагонали квадрата перпендикулярны (BD ⊥ AC), диагонали квадрата равны (BD = AC); диагонали квадрата являются биссектрисами углов.
Ученики заполняют пропуски в схеме и проверяют правильность заполнения (Приложение №3) на раздаточном листе и оставляют этот лист у себя, чтобы пользоваться этой схемой на уроках.
Итак, давайте еще раз повторим все, что мы знаем о квадрате.
Ребята, для того, чтобы привести в систему все ваши знания о параллелограммах и их свойствах, посмотрите внимательно на следующую схему. (Приложение №2)
Заполнить в данной схеме пропуски, вместо которых записать, используя математические обозначения, определения или свойства параллелограммов.
Аргументация своего мнения и позиции в коммуникации; учёт разных мнений (К)
Оценивание усваемого содержания (Л)
Рефлексия способов и условий действия (П)
Оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения
6. Итог урока (рефлексия деятельности)
Цель: осознание учащимися своей учебной деятельности, самооценка результатов деятельности своей и всего класса
Задачи: Организация групповой рефлексии относительно достижения учебных целей в форме полилога
Оценивают свою деятельность, понимая нужную фигуру.
Покажите на сигнальных карточках: квадрат – да, ромб – не очень, прямоугольник– нет:
- Доволен ли ты как прошел урок?
- Было ли тебе интересно?
- Сумел ли ты получить новые знания?
- Был ли ты активен на уроке?
- Сумел ли ты показать свои знания?
Рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности (П)
Самооценка; адекватное понимания причин успеха или неуспеха в УД; следование в поведении моральным нормам и этическим требованиям (Л)
Выражение своих мыслей полно и точно; формулирование и аргументация своего мнения, учёт разных мнений (К)
7.Задание на дом
Цель: на основе выявленных результатов дать домашнее задание, которое развивало бы и закрепляло знания учащихся
Задачи: На основе выявленных результатов дать домашнее задание, которое развивало бы и закрепляло знания учащихся.
Деятельность учащихся
Деятельность учителя
Формируемые УУД
Записывают домашнее задание
Достаньте свои дневники и запишите домашнее задание.
Творческое задание: сочинить мини – сказку о любой геометрической фигуре;
на «3» – №399,
на «4» – №399, №405,
на 5» – №399, №405, №411
Источник
