Что такое кривые безразличия и какими свойствами они обладают

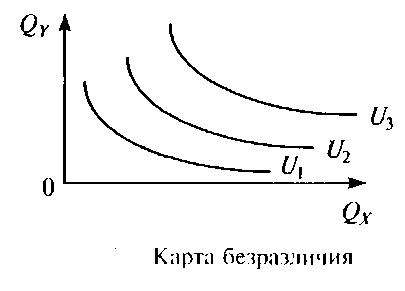
График карты кривых безразличия.
Кривая безразличия — множество всевозможных комбинаций благ, имеющих для потребителя одинаковую полезность и по отношению к выбору которых он безразличен. В простейшем двумерном случае кривую безразличия часто изображают на плоскости в виде выпуклой (к началу координат) линии. Однако кривая имеет такой вид лишь при выполнении ряда условий (см. свойства). Понятие кривой безразличия восходит к Фрэнсису Эджуорту и Вильфредо Парето.
Аналогом понятия кривой безразличия для производителя является изокванта — множество всевозможных комбинаций факторов производства. В простейшем случае в качестве факторов используют труд и капитал.
Кривые безразличия явно или неявно возникают при решении задачи потребителя.
Проблема оценки потребителем полезности благ[править | править код]
Поведение потребителя зависит от двух составляющих: рационализм и иррационализм. Под рационализмом понимается логическая обоснованность каких-либо действий. Иррационализм включает в себя совершение действий под воздействием каких-либо чувств, эмоций, инстинктов, рефлексов и так далее. Целью изучения поведения потребителя является определение предсказуемости его поступков. Однако иррациональная часть поведения в настоящее время является малоизученной и малопредсказуемой. Поэтому можно утверждать, что абсолютно точно предсказать поведение потребителя невозможно. В связи с тем, что иррациональность сложно систематизировать и оценить, в классической экономике предпочитают рассматривать только рациональное поведение потребителя. Оно состоит в сопоставлении результатов потребления и затрат. В качестве результатов рассматриваются изменения полезности, в качестве затрат — суммы денег, потраченные на покупки. Так как в экономике для анализа используются цифры, то первоначально была предпринята попытка оценки полезности. Учёные (Уильям Джевонс, Карл Менгер, Леон Вальрас), которые придерживались данного подхода, назывались кардиналистами. Они понимали, что существует субъективность в оценках различных людей, поэтому пользовались методом индукции, рассматривая оценку среднего потребителя. Благодаря кардиналистам была исследована динамика общей предельной полезности. Другая группа учёных — ординалисты, считали подход кардиналистов неправильным из-за таких обстоятельств как: 1) неспособность точной цифровой оценки, из-за несовершенства информации; 2) переменчивость взглядов потребителя во времени. Взамен точной оценке, ординалисты предложили относительную оценку, которая не нуждалась в цифровой оценке полезности.
Эффект дохода и эффект замещения[править | править код]
Эффект дохода — это результат воздействия на спрос потребителя изменения его реального дохода, вызванного изменением цены товара, без учёта эффекта замещения. Эффект замещения — изменение структуры потребления в результате изменения соотношения цен товаров при неизменном реальном доходе.
Разделение эффекта цены на эффект дохода и замещения позволяет проводить оценку товаров по отношению к доходу. Эффект замещения всегда имеет одно направление: в случае снижения цены он положительный, в случае увеличения — отрицательный. В то же время эффект дохода имеет разное направление: в случае снижения цены эффект дохода положителен, общий эффект цены положительный, значит речь идёт о нормальных товарах. Если в случае снижения цены, эффект дохода отрицательный, а общий эффект положительный, то речь идёт об инфериорных товарах. Если в случае снижения цены эффект дохода отрицательный, общий эффект отрицательный (то есть эффект дохода больше эффекта замещения), то это товар Гиффена.
Практическое значение анализа кривых безразличия[править | править код]
Анализ кривых безразличия используется для определения потребностей различных потребителей с целью изменения различных товаров и услуг. Под видом кривых безразличия подразумевается структура расходов населения, а в случае изменения доходов, каково изменение данной структуры. Также анализ кривых безразличия может быть использован в различных частных ситуациях, связанных, например с осуществлением выбора, в качестве представителя различных направлений социальной политики, в случае подбора различных подарков и т. д.
Формальное определение[править | править код]
Кривая безразличия — это линия (поверхность, гиперповерхность) уровня функции полезности .
При различных (допустимых) значениях константы получается семейство кривых, которое обычно именуется картой безразличия. Математически карта безразличия — это фактормножество в пространстве альтернатив.
Свойства кривых безразличия[править | править код]
Свойства кривых безразличия зависят от свойств функции полезности, которая в свою очередь определяется лежащим в её основе предпочтением.
- Кривые безразличия не могут пересекаться, поскольку не пересекаются линии уровня функции полезности.
- Если предпочтения являются монотонными, то каждая следующая кривая безразличия, проходящая дальше от начала координат, отражает бо́льшую величину полезности, чем предыдущая.
- Из-за монотонности предпочтений кривые безразличия имеют отрицательный наклон.
- Если предпочтения удовлетворяют свойству локальной ненасыщаемости, то кривые безразличия являются «тонкими».
- Предельная норма замещения MRS одного блага другим уменьшается при движении вдоль кривой безразличия, а сами кривые безразличия являются вогнутыми по отношению к началу координат. Это свойство связано с выпуклостью отношения предпочтения (квазивогнутостью функции полезности).
Примеры кривых[править | править код]
Примеры кривых для наиболее распространённых функций полезности.
Форма кривых для «обычных товаров», обладающих частичной заменяемостью.
Встречаются экзотические примеры «кривых» безразличия. Например, карта безразличия для лексикографических предпочтений состоит из отдельных точек.
Литература[править | править код]
- Bruce R. Beattie and Jeffrey T. LaFrance, «The Law of Demand versus Diminishing Marginal Utility» (2006). Review of Agricultural Economics. 28 (2), pp. 263—271.
- Volker Böhm and Hans Haller (1987). «Demand Theory», The New Palgrave: A Dictionary of Economics, v. 1, pp. 785-92.
Источник
Предположим, что потребитель имеет набор благ, состоящий из X и Y. Все соотношения количеств этих благ для него равноценны, потребителю безразлично, какой набор выбрать. Следовательно, эти товары принадлежат к набору безразличия. Набор безразличия — набор вариантов потребительского выбора, каждый из которых обладает одинаковой полезностью и поэтому не имеет предпочтения перед другими.
Кривая безразличия является графическим отображением набора безразличия. Кривая безразличия — совокупность наборов благ, обеспечивающих потребителю равный объем удовлетворения потребностей, т. е. приносящих ему одинаковую полезность. Взяв другие возможные сочетания благ, соответствующие различным величинам совокупной полезности, можно составить карту безразличия. Карта безразличия — совокупность кривых безразличия, соответствующих различным уровням полезности для одного потребителя и одной пары благ. Вкусы и предпочтения потребителя представляются картой кривых безразличия. Каждая следующая кривая безразличия, проходящая дальше от начала координат, предполагает относительно большую величину полезности.
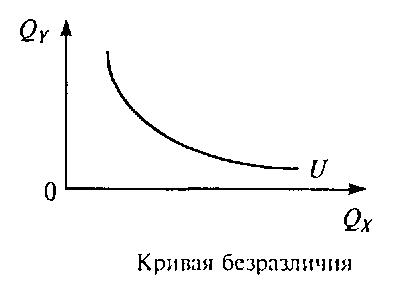
Любая кривая безразличия представляет одинаковую совокупную полезность различных благ для потребителя. Кривая безразличия (U) состоит из точек, символизирующих наборы товаров Х и Y. Совокупные полезности всех наборов, представленные точками на этой кривой одинаковы, т. е. потребителю безразлично, какую именно комбинацию товаров Х и Y он приобретет. Переходя от точки А к точке В, потребитель сокращает потребление блага Y на ?Y и наращивает потребление товара X на ?Х, но общий уровень удовлетворения потребителя (совокупная полезность) остается неизменным (рисунок ниже).
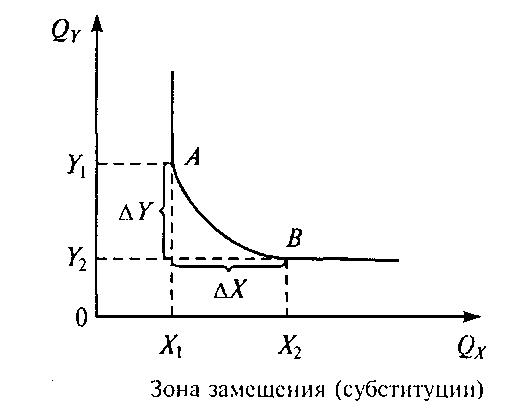
Зона замещения (субституции) — участок кривой безразличия, на котором возможна эффективная замена одного блага другим.
Взаимная замена благ X и Y возможна только в пределах отрезка АВ (зоне замены). Количество блага Х1 представляет минимально необходимое количество потребления блага X, от которого потребитель не может отказаться, как бы много товара Y ни предлагалось взамен. Аналогично Y1 — минимально необходимое количество потребления блага Y. Предельная норма замещения — норма, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя. Предельная норма замещения — количество одного блага, от которого потребитель готов отказаться, чтобы получить дополнительную единицу другого блага. Предельная норма замещения рассчитывается следующим образом:
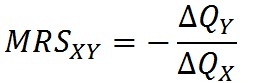
где MRS — предельная норма замещения; Qx — количество товара X; QY — количество товара Y.
Предельная норма замещения всегда отрицательная величина, так как прирост потребления одного блага происходит за счет сокращения потребления другого. Предельная норма замещения уменьшается при движении вдоль кривой безразличия — получая в свое распоряжение все большее количество данного блага и наращивая его потребление, покупатель в обмен готов отказаться от все меньшего количества другого блага, которое становится все более дефицитным. У потребителя, желающего остаться на той же кривой безразличия, прирост полезности от наращивания потребления блага X должен быть равен потере полезности от сокращения потребления товара Y. Таким образом, предельная норма замещения блага X благом Y может рассматриваться как отношение предельной полезности блага X к предельной полезности блага Y:
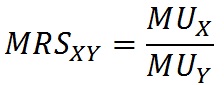
Рассмотрим некоторые свойства кривых безразличия:
• кривые безразличия имеют отрицательный наклон. Между количествами благ X и Y существует обратная связь. При уменьшении потребления одного блага, для компенсации потерь и сохранения прежнего уровня полезности, потребитель должен увеличить потребление другого блага. Любая кривая, выражающая обратную связь переменных, имеет отрицательный наклон;
• кривые безразличия выпуклы по отношению к началу координат. Выше отмечалось, что при увеличении потребления одного блага потребитель должен уменьшить потребление другого блага. Выпуклость кривой безразличия по отношению к началу координат является следствием падения предельной нормы замещения. Пологий спуск кривой безразличия вниз или подъем наверх свидетельствует об убывании темпов замещения одного блага другим по мере уменьшения доли данного блага в потребительской корзине;
• абсолютная величина наклона кривой безразличия равна предельной норме замещения. Угол наклона кривой безразличия в данной точке показывает норму, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя. Данное соотношение характеризуется предельной нормой замещения;
• кривые безразличия не пересекаются. Один и тот же потребитель не может характеризовать один и тот же набор благ различными уровнями полезности. Следовательно, две кривые безразличия, представляющие различные уровни полезности, не могут пересечься;
• возможно построить кривую безразличия, проходящую через любой набор благ. Кривую безразличия можно построить для любой пары благ, приносящих определенный уровень полезности. Именно по этому принципу строится карта безразличия, дающая полную информацию о системе предпочтений потребителя.
Источник
Понятия «кривая безразличия», «бюджетное ограничение» используются в экономической теории в рамках ординалистической теории полезности. Их появление было связано с необходимостью устранить недостаток кардинатистической теории, которая измеряла полезность в абсолютном выражении, тогда как при ординалистическом подходе используется относительное измерение полезности благ, сравнение их друг с другом. Теорию развивали Ф. Эджуорт, В. Парето, И. Фишер.
Кривые безразличия
Кривая безразличия (КБ) представляет собой графическое изображение выбора потребителя между двумя благами.
Положение каждой точки этой кривой характеризует такую комбинацию из двух товаров или услуг (по оси х и у), которая приносит одинаковую полезность индивиду.
Другими словами, полезность комбинации А равна полезности комбинации В, и потребителю безразлично, какую из них выбрать. Например, ученик использует карандаши и ручки, и ему будет не важно, выбрать пенал А, в котором лежат 3 ручки и 7 карандашей, или пенал В, где 4 ручки и 6 карандашей.
Свойства кривых безразличия
Кривые безразличия не пересекаются. Это связано с тем, что каждая КБ описывает свой уровень полезности. Математически они представляют собой линии уровня функции полезности, то есть, зафиксировав U, строят ту или иную кривую, форма которой не меняется, а будет изменяться только положение.
Чем больше расстояние от кривой до начала координат, тем выше полезность наборов, которым она соответствует. При увеличении общей полезности набора благ происходит сдвиг КБ вверх вправо, а при уменьшении – вниз влево. На основании приведенного ниже графика это свойство можно описать так: набор благ на U более предпочтителен, чем на U2, но менее предпочтителен, чем на U1.
Кривая безразличия вогнута к началу координат, вследствие этого любая касательная, проведенная к ней, будет иметь отрицательный наклон. Такая форма КБ связана с тем, что при увеличении количества потребляемого блага, полезность каждой дополнительной единицы убывает. Также в силу рациональности индивида предпочтение всегда отдается большему количеству товаров и услуг, чем меньшему.
Бюджетное ограничение и потребительский выбор
Каждый индивид имеет в своем распоряжении определенный размер денежных средств, которые он тратит на ту комбинацию товаров или услуг, которые изображаются кривой безразличия. Эта сумма денег и есть бюджетное ограничение, которое накладывается на выбор потребителя.
Например, у Васи есть 200 д.е., цена пирожка с капустой 50 д.е., а пирожка с мясом 100 д.е. На свои деньги он сможет купить следующие наборы пирожков (4 с капустой; 0 с мясом), (2К; 1М), (0К;2М). Эти точки и будут лежать на прямой, описывающей бюджетное ограничение.
Представим это на графике.
Оптимальный выбор потребителя будет находиться в точке касания бюджетной линии к кривой безразличия.
Если рассматривать математическую интерпретацию задачи оптимального выбора, то необходимо использовать понятие предельной полезности.
Пусть U=f(x,y)U=f(x,y)U=f(x,y) – функция полезности.
MUx=fx′MU_x= f’_xMUx=fx′
MUy=fy′MU_y= f’_yMUy=fy′
Тогда оптимум будет достигаться при
MUxPx=MUyPyfrac{MU_x}{P_x}=frac{MU_y}{P_y}PxMUx=PyMUy
Примеры решения
Пример 1
Сидоров Степан Сергеевич вышел на пенсию и решил, что 1000 руб. из нее он будет тратить только на творог и сыр. Стоимость пачки творога составляет 20 руб., сыра — 50 руб. Также, имея за плечами опыт экономиста, он определил, что функция полезности этих продуктов U=x⋅yU=xcdot yU=x⋅y. Теперь перед ним стоит задача, в каком объеме покупать творог и сыр, чтобы достичь максимальной полезности и потратить всю выделенную для этого сумму.
Решение
Находим предельные полезности.
MUx=yMU_x= yMUx=y
MUy=xMU_y= xMUy=x
Тогда
y20=x50frac{y}{20}=frac{x}{50}20y=50x
x=2,5yx=2,5yx=2,5y
С учетом максимальных трат на эти продукты Степана Сергеевича в размере одной тысячи рублей:
20x+50y=100020x+50y=100020x+50y=1000
50y+50y=100050y+50y=100050y+50y=1000
y=10y=10y=10
x=2,5⋅10=25x=2,5cdot10=25x=2,5⋅10=25
То есть он будет покупать 10 пачек сыра и 25 пачек творога.
Пример 2
Доход Клавдии Петровны составляет 7500 руб., из них 450 руб. она выделяет на покупку корма коту Барсику и собаке Джеку. Цена корма для котов составляет 20 руб. за 1 кг, а для собак — 15 руб. за кг. Составить уравнение бюджетного ограничения.
Решение
Если Клавдия Петровна всю сумму потратит на кошачий корм, то она купит
x=450/20=22,5x=450/20=22,5x=450/20=22,5 кг
Значит, прямая бюджетного ограничения будет проходить через точку (22,5;0)
Аналогично по собачьему корму
y=450/15=30y=450/15=30y=450/15=30 кг
То есть прямая проходит через (0;30)
Из математики мы знаем уравнение прямой, проходящей через две точки
x−x1x2−x1=y−y1y2−y1frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}x2−x1x−x1=y2−y1y−y1
x−22.50−22.5=y−030−0frac{x-22.5}{0-22.5}=frac{y-0}{30-0}0−22.5x−22.5=30−0y−0
y=30−4/3xy=30-4/3xy=30−4/3x
Тест по теме «Кривые безразличия и их свойства»
Источник
Свойства кривых безразличия следуют из тех аксиом, на которых базируется ординалистский подход:
- • наборы на кривых безразличия, более удаленных от начала координат, обеспечивают потребителю более высокую полезность. Это вытекает из предположения, что большее количество благ предпочитается меньшему количеству;
- • кривые безразличия не могут пересекаться, так как являются геометрическим местом наборов равной полезности; точка пересечения означала бы равенство полезности разноудаленных кривых;
- 1 Впервые применены английским экономистом Ф. Эджуортом в 1881 г.
- • касательная, проведенная к любой точке кривой безразличия, имеет отрицательный угол наклона.
Набор кривых безразличия для одного потребителя и для одной пары благ образует карту безразличия. На карте безразличия (рис. 4.2) А, В, С, D — товарные наборы, состоящие из двух товаров X и У. Наборы А и В (С и D), расположенные на кривой безразличия U1(U2)y включают неодинаковые количества первого и второго благ. Однако для потребителя эти наборы равноценны, безразличны, так как их потребление принесет ему равную полезность U(U2).

Рис. 4.2. Карта кривых безразличия
По аксиомам порядковой теории полезности: С ~ D; А ~ В] С > A; D > В; U2 > U{. Осуществляя выбор, рациональный потребитель располагает наборы благ в соответствии со своими предпочтениями, т.е. ранжирует. Он может присвоить каждому набору число, соблюдая правило: более предпочтительному набору — большее число, менее предпочтительному — меньшее. В этой процедуре важным остается соотношение чисел, а не сами числа. Задать числа можно произвольно или по формуле, используя функцию. Зависимость общей полезности от количества благ в потребительских наборах назовем функцией полезности.
Порядковая, или ордипалистская, функция полезности — это способ приписывания наборам благ определенных значений полезности.
На рис. 4.2 любая рыночная корзина на кривой /У2, такая как С, является более желанной, чем любая корзина на кривой Uv например корвина А. Однако величину, на которую А предпочтительнее С, нельзя вычислить на основании карты кривых безразличия или с помощью порядковой функции полезности, которая порождает эту карту.
Порядковая функция полезности должна соответствовать всем указанным выше аксиомам. Она описывается непрерывной математической зависимостью, допускающей монотонные преобразования. Например, умножение данной функции на положительное число, прибавление к функции любого числа. Результирующая функция должна отвечать всем свойствам первоначальной функции.
Для набора, состоящего из двух благ X и Y, функция полезности U имеет вид:

где F — символ функции, показывающий, что U (уровень полезности) зависит от переменных, заключенных в скобки.
Функция полезности U предполагает, что полезность, получаемая человеком, зависит только от количества товаров X (Qx) и Y (Qy), потребляемых за определенный период, например неделю. Функция полезности может включать сколько угодно переменных, но в экономической литературе используется двухпродуктовая модель.
В отличие от кардиналистской функции полезности TU = F (Qa, Qb, …, Qz), измеряющей полезность какого-либо количества благ в утилитах, порядковая (ординалисгская) функция полезности имеет вид U = F (X, Y), где количество переменных задает размер набора (в нашем случае — набор из двух благ), а количество каждого из благ позволяет ранжировать наборы.
Предельные полезности первого и второго благ, входящих в набор, можно представить зависимостями

Предельная полезность MUг-го блага показывает приращение полезности набора при изменении объема потребления i-го блага на единицу и при неизменном объеме потребления других благ.
Потребитель может изменить структуру своего потребления, замещая некоторое количество одного блага другим благом и сохраняя неизменным уровень полезности набора.

Рис. 4.3. Кривая безразличия
Предположим, что потребитель желает получить определенный уровень полезности U (X, Y) = X, Y от набора, допуская сочетание в нем разных количеств двух благ: набор а (1; 12), набор б (2; 6); набор в (3; 4); набор г (4; 3). Кривая безразличия с такими наборами благ изображена на рис. 4.3.
Имея набор а, потребитель согласен отказаться от шести единиц второго блага Y в обмен на увеличение первого блага X на одну единицу при сохранении прежнего уровня полезности U.
Предельная норма замещения (marginal rase of substitution, MRS) двух благ показывает, сколько единиц второго блага У потребитель готов обменять на одну единицу первого блага X, чтобы сохранить неизменным уровень полезности.
Это выражается формулой

Поскольку X и Y изменяются в разных направлениях, то предельная норма замещения двух благ (MRSxy) имеет отрицательный знак, показывая, каким количеством блага Y (-) готов пожертвовать потребитель, чтобы приобрести еще одну единицу блага X (+).
Предельная норма замещения характеризует индивидуальную норму обмена двух благ. В нашем примере потребитель, переходя от набора а к набору б, имеет MRSxy = 6, от набора б к набору в — MRSU = 2, от набора в к набору г — MRSxy = 1.
Предельная норма замещения двух благ равна наклону (по абсолютной величине) кривой безразличия соответственно на участках аб, бв, вг и т.д. При достаточно малых изменениях АХ и ДК предельная норма замещения равна наклону касательной линии, проведенной к кривой безразличия в этой точке.
При движении сверху вниз вдоль кривой безразличия предельная норма замещения двух благ убывает.
Изменения полезности, которые вызваны уменьшением количества второго блага MUy • А У, AY Мих • АХ, АХ > 0, компенсируют друг друга. В результате общий уровень полезности не меняется:

Следовательно, предельная норма замены блага Y благом X может рассматриваться, как отношение предельной полезности блага X к предельной полезности блага Y. Поскольку MUX уменьшается по мере замены товаром X товара У, a MUyy соответственно, увеличивается, отношение MUx/MUy, равное MRSxyy уменьшается.
Графически это проявляется как убывание углового коэффициента наклона касательной по мере движения вниз вдоль кривой безразличия, что объясняет гиперболический вид кривых безразличия. Уменьшающаяся предельная норма замены в порядковой теории имеет тот же смысл, что и убывающая предельная полезность в количественной теории. Только во втором случае полезность каждой дополнительной единицы товара оценивается в утилитах, а в первом – объемом другого товара, от которого потребитель готов отказаться.
Однако условие уменьшающейся предельной нормы замены не всегда соблюдается. Для товаров, жестко взаимодополняющих друг друга (ботинки и шнурки к ним), кривые безразличия имеют 2,-образный вид (рис. 4.4, а). Здесь MRSxy – 0, так как эти блага не могут заменяться. Нулевая предельная норма замены и норма замены, равная бесконечности, характерна и для тех ситуаций, когда потребитель не поступится даже бесконечно малым количеством товара в пользу другого.

Рис. 4.4. Кривые безразличия абсолютно взаимодополняемых (а) и взаимозаменяемых (б) благ
Для двух абсолютно взаимозаменяемых товаров (кофе и чай для конкретного потребителя) кривые безразличия представляют собой прямые линии (рис. 4.4, б), имеющие отрицательный наклон. Это случай, когда оба товара воспринимаются потребителем как один, и MRS — постоянная величина.
Источник
