Что такое диаметр и какими свойствами он обладает

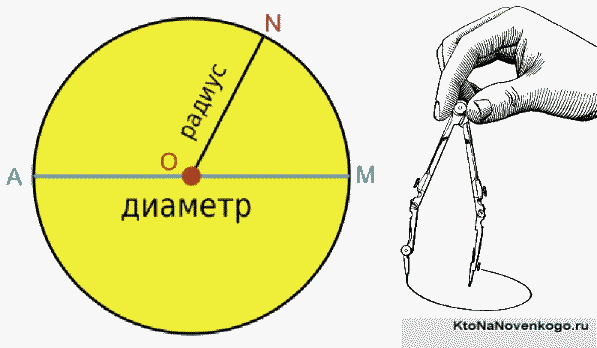
Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Обобщённо диаметром фигуры (множества) называется максимальное расстояние между точками этой фигуры (множества), или точная верхняя грань всевозможных расстояний, если максимальное не существует.

Диаметр геометрических фигур[править | править код]

Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Символ диаметра[править | править код]

Символы со сходным начертанием: Ø · ø · ∅

Диаметр принято обозначать символом [1].
Символ диаметра представлен в Юникоде (U+2300 ⌀ diameter sign)[2] и, хотя он отсутствует в стандартных раскладках клавиатуры, может быть введён с клавиатуры:

в HTML как ⌀ или ⌀
в LaTeX его обозначает команда diameter из пакета wasysym
в Microsoft Word символ можно получить, введя 2300 и нажав Alt+X
в Windows с помощью Alt-кода Alt+8960
в системах, использующих X Window System (Unix/Linux/ChromeOS и др.), с помощью комбинации Ctrl+⇧ Shift+u 2300Пробел или с использованием клавиши Compose, нажав поочерёдно Composedi[3].

Также, символ можно найти и скопировать в приложениях и инструментах типа «таблица символов», например:

в Windows — Таблица символов[en]
в программах из пакета Microsoft Office — меню «Вставка» → «Символ…»
в macOS — Character Palette/Viewer (вызывается комбинацией ⌥ Opt+⌘ Cmd+T)
в GNOME — Таблица символов GNOME (ранее — gucharmap).

Во многих случаях символ диаметра может не отображаться, так как его редко включают в шрифты (он присутствует, например, в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других), в связи с чем вместо него часто используются другие символы со схожим начертанием. К примеру, в САПР AutoCAD вместо символа диаметра используется символ пустого множества (U+2205 ∅ empty set), вводящийся сочетанием %%c (буква c — латинская) или U+2205 в текстовой строке. Того же подхода придерживается в своих стандартах и консорциум W3C[4]. Также, для замены часто используется буква Ø датско-норвежского алфавита.

Сопряжённые диаметры эллипса и гиперболы[править | править код]

Сопряжённые диаметры эллипса[править | править код]

Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм

Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

На рисунке представлена пара сопряжённых диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зелёные линии на рисунке).

Сопряжённые диаметры гиперболы[править | править код]

Для произвольного угла φ показаны диаметры и сопряжённые им диаметры для окружностей и равнобочных гипербол.

Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
В случае гипербол с асимптотами, образующими прямой угол, её сопряжённые гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряжённый диаметр, который будет просто диаметром сопряжённой гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряжённых диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряжённых диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).

Вариации и обобщения[править | править код]

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические и математические объекты. Если во множестве некоторых объектов определена метрика пространства, то для подмножества этих объектов может быть введено понятие диаметра множества.

Диаметром множества , лежащего в метрическом пространстве с метрикой , называется величина .

Под диаметром метрического пространства понимается точная верхняя грань расстояний между парой любых его точек.

В частности:

Например, диаметр n-размерного гиперкуба со стороной s равен

Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре[править | править код]

Окружность Фурмана построена на одном отрезке, как на диаметре
Окружность Брокара построена на одном отрезке, как на диаметре

См. также[править | править код]

Радиус
Пи
При делении фигур на части меньшего диаметра возникла гипотеза Борсука, опровергнутая в 1993 году
Изодиаметрическое неравенство
Угловой диаметр астрономических объектов.
Диаметр циркуляции

Литература[править | править код]

Диаметр // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

↑
Большаков В. П., Тозик В. Т., Чагина А. В. Инженерная и компьютерная графика. — СПб.: БХВ-Петербург, 2013. — 288 с. — ISBN 978-5-9775-0422-5. — С. 90.
↑
The Unicode Standard, Version 13.0. Miscellaneous Technical, Range: 2300–23FF (англ.) (PDF). Unicode Inc[en] (2020). Дата обращения 6 сентября 2020.
↑
Monniaux, David UTF-8 (Unicode) compose sequence (англ.). — Файл конфигурации вводимых с помощью клавиши Compose символов. Дата обращения 6 сентября 2020.
↑ https://www.w3.org/Math/characters/html/symbol.html

Источник

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такое ДИАМЕТР. Это одно из базовых понятий в математике, которое начинают изучать еще в 3-м классе.

Но и повседневной жизни он встречается настолько часто, что знать его просто необходимо.

Диаметр — это…

Диаметр – это в первую очередь, хорда. Так называют отрезок (что это?) прямой, который соединяет две определенные точки. В нашем случае эти точки располагаются на максимально отдаленном друг от друга расстоянии на окружности, благодаря чему хорда проходит через ее центр.

В то же время диаметром еще называют и длину это самой хорды. Кстати, аналогичные определения применимы не только к окружностям, но и к другим геометрическим фигурам, таким как шар или сфера.

Графически это выглядит вот так:

Само слово «диаметр», как и многие термины в нашем языке, пришло из Древней Греции. Ведь именно в этой стране жили прославленные математики, такие как Евклид, Пифагор, Архимед, Платон. Так вот, греческое слово «διάμετρος» можно перевести как «поперечник».

Интересно, что во многих современных языках есть также похожие слова. Например, на латыни это «diametrus», во французском «diamètre», в немецком «diamétral». А в русском языке мы нередко употребляем слово «диаметральный».

Например, говорим «диаметральные взгляды» или «диаметральные точки зрения», подразумевая совершенно противоположное отношение к чему-либо. Ну, точно как противоположные точки на окружности, разделенные диаметром.

Обозначения и символ диаметра

Диаметр имеет несколько сокращенных обозначений.

Например, если речь идет о математике, то в ней чаще всего употребляется латинская буква «D». Причем допускается как прописное написание этой буквы, так и строчное – «d». Второй вариант даже чаще встречается в задачках.

Например, это может выглядеть так:

d = 12 см или D = 12 см

А вот если говорить о бытовом понятии «диаметра», то тут уже чаще используется другой символ. Это – перечеркнутая буква «О».

Именно такой знак вы наверняка увидите, когда речь идет о трубах, о размере сверла и так далее. И записываются они так:

Ø6, Ø8, Ø12, Ø15, Ø20, Ø100

По умолчанию считается, что подобные обозначения всегда считаются в миллиметрах.

Стоит сказать, что символа «Ø» нет на обычной раскладке клавиатуры. И чтобы напечатать его в тексте, нужно или открыть специальный раздел «дополнительные символы» в программе Word, или просто скопировать откуда-нибудь, а потом вставить.

Радиус и другие величины, связанные с диаметром

Главной величиной, которая неизменно связана с диаметром, является радиус.

Радиус – это расстояние от центра окружности до любой точки на дуге окружности. Соответственно, радиусом также называют и длину этого отрезка.

Радиус обозначается буквой «R» или «r». И он всегда равен половине диаметра. В математике это уравнение записывают как:

D = 2R или R = D/2

Еще одна важная величина – длина окружности. Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой:

С = 2πR или С = πD

Где «π», как многие знают, это математическая константа. И считать ее принято как 3,14, хотя после запятой там бесконечное количество знаков.

И наконец, еще одна величина – площадь окружности (круга). Это размер всего, что находится внутри ее границ. Обозначается она буквой «S». И чтобы ее вычислить, опять же надо воспользоваться определенной формулой:

S=πR²

Соответственно, эти формулы можно и перевернуть. То есть, зная длину или площадь окружности, всегда можно высчитать ее диаметр.

Интересные факты о диаметре

Первое документальное упоминание слова «диаметр» в России относится к 1720 году. И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах.

Диаметр Земли составляет 12 543 километра. Это огромное расстояние. Но и оно кажется маленьким, если сравнить, например, с Солнцем. А у него диаметр составляет 1 390 000 километров, что в 109 раз больше земного.

Диаметр 10-копеечных монет в нашей стране не менялись на протяжении сотни лет. Он составляет 17,5 миллиметров. Таким он был еще при Николае II, таким же и в советское время, таким же остался и сейчас.

Вот и все, что мы хотели рассказать о таком понятии, как диаметр. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

ВоркЗилла – удаленная работа для всех
Анкетка – платят за прохождение тестов
Etxt – платят за написание текстов
Кьюкоммент – биржа комментариев
Поиск лучшего курса обмена
60сек – выгодный обмен криптовалют
Бинанс – надёжная биржа криптовалют
ВкТаргет – заработок в соцсетях (ВК, ОК, FB и др.)

Источник

Диаметр геометрических фигур

Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Символ диаметра

Символы со сходным начертанием: Ø · ø · ∅

Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов» (ранее gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или U+2205 в текстовой строке.

Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.

Сопряжённые диаметры эллипса и гиперболы

Сопряжённые диаметры эллипса

Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

На рисунке представлена пара сопряженных диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зеленые линии на рисунке).

Сопряжённые диаметры гиперболы

Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.

Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
В случае гипербол с асимптотами, образующими прямой угол, её сопряженные гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряженный диаметр, который будет просто диаметром сопряженной гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряженных диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряженных диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).

Вариации и обобщения

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.

Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:

Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре

Окружность Фурмана построена на одном отрезке, как на диаметре
Окружность Брокара построена на одном отрезке, как на диаметре

См. также

Радиус
Пи
При делении фигур на части меньшего диаметра возникла гипотеза Борсука, опровергнутая в 1993 году
Изодиаметрическое неравенство
Угловой диаметр астрономических объектов.
Диаметр циркуляции

Литература

Диаметр // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Источник

Что такое окружность?

Окружность — одна из самых важных кривых линий на плоскости, её можно начертить циркулем или даже натянутой верёвкой, если закрепить один из концов верёвки в данной точке. В любом случае расстояние от всех точек окружности до данной закреплённой точки будет одинаково. Эту точку называют центром окружности, а любой отрезок, который соединяет точку на окружности с её центром, называется радиусом. В переводе с латыни слово радиус означает “спица колеса”. Это не удивительно, ведь можно сказать, что окружность — это математическая модель колеса. Если две любые точки окружности соединить отрезком, то получится хорда. Хорда же в переводе с греческого языка означает “струна”. Если хорда проходит через центр окружности, то её называют диаметром и обычно обозначают буквой . Понятно, что длина диаметра окружности должна быть равна двум её радиусам, то есть . Давайте повторим ещё раз.

Определения.

Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки.

Радиус окружности — отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны.

Хорда окружности — отрезок, соединяющий две любые её точки.

Диаметр окружности — это хорда, которая проходит через центр окружности.

Свойство диаметра.

Легко доказать, что диаметр окружности — это самая длинная её хорда. Да, и само слово диаметр в переводе означает “поперечник”. В технике измеряют диаметры колёс, труб, винтов и гвоздей и обозначают их таким значком .

Давайте сформулируем данное свойство диаметра как теорему.

Теорема.

Любая хорда окружности не превышает её диаметра.

Доказательство. Возьмём на окружности с центром в точке и радиусом любые две точки и . Если хорда проходит через центр окружности, то по определению она будет её диаметром и равна . Если же хорда не содержит центра окружности, то образуется треугольник . Тогда для него должно выполняться неравенство треугольника: . Значит, в любом случае хорда не может быть больше диаметра окружности. Что и требовалось доказать.

Полезно знать, что в геометрии диаметр можно определить не только для окружности или круга. Он есть у квадрата, треугольника, да и вообще у многих других геометрических фигур. А знаете, что называют диаметром фигуры? Так же, как и у окружности, диаметр фигуры — это самая длинная её хорда.

Определение.

Диаметр геометрической фигуры — это самое большое расстояние между любыми двумя точками этой фигуры.

Что такое круг?

Чем круг отличается от окружности? Каждый человек интуитивно понимает, что круг — это то, что находится “внутри ” окружности. Можно даже сказать, что для окружности круг — это её внутренняя область. Правда, работать с таким определением не очень удобно.

Как же можно удобно определить круг? Предположим, что один фермер выпустил пастись свою козу на луг, а чтобы она далеко не ушла, привязал её к колышку в точке с помощью верёвки длины . В течение дня коза выщипала траву везде, куда она смогла дотянуться. Как выглядит та часть луга, где паслась коза, и где теперь не стало травы?

Ясно, что коза не сможет отойти от колышка, к которому она привязана, дальше чем на длину своей верёвки. И она сможет дотянуться до любого места, которое ближе находится к этому колышку, чем длина её верёвки. Таким образом, коза выщиплет траву внутри круга с центром в точке и радиусом , равным длине её натянутой верёвки. Теперь мы с вами уже можем дать следующее определение.

Определение.

Круг — это множество всех точек плоскости, удалённых от данной точки не более, чем на длину данного отрезка.

Данная точка называется центром круга, а указанный отрезок — радиусом круга.

Круг с центром в точке и радиусом обозначают так: круг .

Разберём несколько примеров решения задач.

Пример 1. В окружности провели две хорды и , равные радиусу этой окружности. Найдите угол .

Решение. Отметим центр данной нам окружности и проведем радиусы в точки , и . Тогда треугольники и будут равносторонними. Значит, их углы и будут равны . Искомый угол равен их сумме, поэтому он будет равен .

Ответ: .

Пример 2. В окружность радиуса вписан квадрат. Найдите площадь этого квадрата.

Решение. Отметим центр данной нам окружности и проведем из него радиусы во все вершины квадрата .

Поскольку у квадрата все стороны равны, а радиусы окружности равны по определению, треугольники , , и будут равны по трём сторонам. Значит, равны все их углы при вершинах в точке . Сумма этих четырёх углов равна , поэтому каждый угол равен .

Запишем теорему Пифагора для треугольника : . Значит, сторона квадрата равна , а его площадь равна квадрату стороны. То есть, она равна .

Ответ: .

Пример 3. В окружность радиуса вписан равносторонний треугольник. Найдите расстояние от центра окружности до стороны этого треугольника.

Решение. Соединим центр окружности с вершинами равностороннего треугольника , который вписан в эту окружность. Поскольку все стороны треугольника равны, а радиусы окружности равны по определению, то равнобедренные треугольники , и будут равны по трём сторонам. Поэтому будут равны шесть углов при основаниях этих треугольников. Обозначим величину каждого из них через и запишем сумму всех углов треугольника : . Откуда .

Расстояние от точки до прямой линии — это длина перпендикуляра, опущенного из этой точки на данную прямую. Давайте опустим из точки перпендикуляр на сторону нашего треугольника и найдём его длину. Треугольник будет прямоугольным, причём его угол при вершине будет равен . Значит, по известному свойству катет против угла равен половине гипотенузы. То есть, .

Ответ: .

Источник