Что такое центр качания каким свойством он обладает
Колебания — это процессы, которые имеют какую либо степень повторяемости во времени.
Свободные (собственные) колебания — это колебания, которые предоставляют сами себе системы, вызванные первоначальным кратковременным внешним возбуждением.
Колебательная система — это такая система, которая способная производить свободные колебания.
Колебательная система соответствует следующим условиям:
- необходимо положение устойчивого равновесия;
- необходим фактор, не позволяющий системе остановиться в положении равновесия в процессе колебаний;
- трение в системе должно быть небольшим, а собственная частота колебательной системы обусловливается только параметрами системы.
Амплитуда колебаний — это максимальное значение величины (для механических колебаний это смещение), которая совершает колебания.
Период колебаний — это самый маленький отрезок времени, через который система совершает колебания, снова возвращается в исходное состояние, т. е. в начальный момент.
Частота колебаний — это физическая величина, равная числу колебаний, которые совершаются в единицу времени.
Циклическая частота — это характеристика гармонических колебаний, совершаемых за
Фаза колебаний — это аргумент функции, который периодически изменяется.
Затухающие колебания — это собственные колебания, у которых амплитуда уменьшается со временем, что обусловлено потерями энергии колебательной системой.
Коэффициент затухания и логарифмический декремент затухания — это характеристика быстроты уменьшения амплитуды в случае механических колебаний, где энергия убывает за счет действия сил трения и других сил сопротивления.
Декремент затухания — это количественная характеристика быстроты затухания колебаний, которая определяется натуральным логарифмом отношения двух последовательных максимальных отклонений 
, колеблющейся величины в одну сторону: 
Декремент затухания — величина, обратная числу колебаний, по истечении которых амплитуда убывает в: е раз е = 2,71828). Промежуток времени, необходимый для этого, называется временем релаксации.
Дифференциальное уравнение малых затухающих колебаний системы: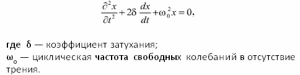
Вынужденные колебания — это колебания, которые возникают под действием внешней периодической силы.
Дифференциальное уравнение вынужденных колебаний:
Резонанс — это процесс резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты 
, вынуждающей силы к собственной циклической частоте 
колебательной системы.
Автоколебания — это незатухающие колебания физической системы, которые способны существовать без воздействия на нее внешних сил.
Автоколебательная система — это физическая система, где имеет место существовать автоколебания.
Автоколебательная система состоит из следующих частей:
- колебательная система, в которой параметры определяют частоту автоколебаний;
- источник энергии, который способствует поддержанию колебаний;
- клапан, который регулирует поступление энергии в колебательную систему;
- положительная обратная связь, которая способна управлять клапаном в колебательной системе.
Обратная связь — это воздействие результатом какого-либо процесса на его протекание.
Обратная связь бывает:
- положительная — это связь, которая приводит к увеличению отклонения;
- отрицательная — это связь, которая приводит к уменьшению отклонения.
Периодические колебания — это колебания, которые имеют изменяющиеся значения физических величин, но которые повторяются через равные отрезки времени.
Смещение — это физическая величина, которая является характеристикой колебаний, равная отклонению тела от положения равновесия в данный момент времени.
Математический, физический, пружинный маятники.
Математический маятник — это тело малых размеров, подвешенное на тонкой нерастяжимой нити, масса которой ничтожно мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести 
уравновешивается силой натяжения нити 
.
Составляющая силы тяжести при отклонении маятника из положения равновесия на некоторый угол ф 
, где знак «минус» означает, что касательная составляющая на- правлена в сторону, противоположную отклонению маятника. Второй закон Ньютона для математического маятника запишется: , где x — линейное смещение маятника от положения равно- весия по дуге окружности, l — радиус.
Угловое смещение будет равно 
Для малых колебаний математического маятника второй закон Ньютона записывается в виде:
Если математический маятник совершает малые колебания, то он является гармоническим осциллятором. Собственная частота малых колебаний математического маятника:
Период малых колебаний математического маятника определяется:
Физический маятник — это тело, которое является твердым, производящее колебания в поле каких-либо сил относительно точки, которая не является центром масс этого тела, или горизонтальной оси.
Второй закон Ньютона для физического маятника принимает вид:
Собственная частота малых колебаний физического маятника:
Период малых колебаний физического маятника определяется:
Круговая частота свободных колебаний физического маятника определяется выражением:
Центр качания физического маятника — это точка, где необходимо сосредоточить всю массу физического маятника, чтобы его период колебаний оставался постоянным.
Физический маятник обладает следующим замечательным свойством: если физический маятник подвесить за центр качания, то его период колебаний будет постоянным, а прежняя точка подвеса станет новым центром качания.
Пружинный маятник — это колебательная система, которая состоит из груза, подвешенного к абсолютно упругой пружине.
Пружинный маятник совершает гармонические колебания с циклической частотой:
, где k — коэффициент жесткости.
Период пружинного маятника определяется:
Уравнение движения пружинного маятника при этом имеет вид:
Источник
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции (рис. 46а). В положении равновесия центр инерции С находится под точкой подвеса 0 маятника на одной с ней вертикали. При отклонении маятника от положения равновесия на угол j возникает вращательный момент сил, стремящийся вернуть маятник в положение равновесия. Этот момент равен
М = –mglsinj,
где m –масса маятника, а l–расстояние между точкой подвеса ицентром масс маятника. Знак “–” означает, что момент сил направлен против углового смещения. Уравнение вращательной динамики принимает вид:
b = М / I = – (mgl/ I) sin j,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса. В случае малых колебаний (j≤ 5°) это уравнение переходит в дифференциальное уравнение собственных незатухающих колебаний:
,
решением которого является функция:
j = А cos (w0t + a0),
где через w0 обозначена угловая частота колебаний:
w0 = (mgl/ I)1/2.
Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, угловая частота w0 которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Период колебаний физического маятника определяется выражением:
.
Из сопоставления формул 
и 
следует, что математический маятник с длиной lпр = (I/ml) имеет такой же период колебаний, как и данный физический маятник. Величину lпр = (I/ml) называют приведенной длиной физического маятника. Итак, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка 0′ на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. По теореме Штейнера момент инерции маятника I может быть представлен в виде
I = I0 + ml2,
где I0 – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника.
Подставив I = I0 + ml2 в lпр = (I/ml) , получаем: lпр = (I0/ml) + l , откуда следует, что приведенная длина lпр всегда больше длины l, так что точка подвеса 0 и центр качания 0′ лежат по разные стороны от центра инерции С (центра масс). Подвесим маятник в центре качания 0′.Приведенная длина в этом случае будет равна: lпр‘ = (I0/ml‘) + l‘ , где l‘ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l‘ = lпр – l, имеем:
lпр‘ = I0/m(lпр – l) + lпр – l = lпр + [(I0 + ml2) – mlпрl] /m(lпр – l).
Выражение, стоящее в квадратных скобках, равно нулю, поскольку I0 + ml2 = I – это момент инерции относительно первоначальной оси вращения; этой же величине равно выражение mlпрl.Таким образом, мы приходим к выводу, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса 0 и центр качания 0′ обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
На свойстве взаимности основано определение ускорения силы тяжести с помощью, так называемого оборотного маятника (рис. 46б). Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы П1 и П2, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжёлые грузы – чечевицы А и В. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно lпр. Измерив период колебаний маятника Т0 и определив lпр, при помощи формулы 
можно найти ускорение силы тяжести g:
.
Источник
Рассмотрим так называемый
математический маятник – материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.
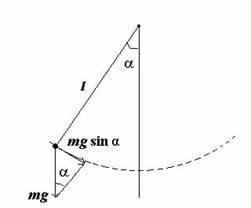
| Второй закон | для такого маятника запишется так: |
,
или
Сравнивая
его с дифференциальным уравнением гармонических
колебаний (2), увидим, что оно по виду будет совпадать, если sina заменить на
a,
что можно сделать при малых a. Следовательно, колебания математического маятника
можно считать гармоническими только при малых углах отклонения от положения
равновесия.
Итак, гармонические колебания математического маятника описываются уравнением
Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси
O (оси качания), не проходящей через центр инерции тела C.
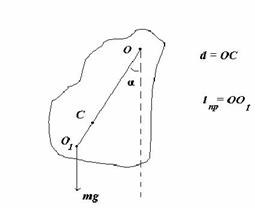
На рисунке обозначено:
ось качания маятника – неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;
точка подвеса маятника О – пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;
приведенная длина физического маятника L пр – длина математического маятника, имеющего такой же период колебаний;
центр качания физического маятника – О1.
Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:
где J – момент инерции маятника относительно точки О.
Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда
sin
a
@
a. В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:
Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:
Из определения приведенной длины физического маятника найдем, что:
Здесь Jc – момент инерции относительно центра масс тела С.
Центр качания О1 обладает тем свойством, что, если ось качания провести через
О1, частота колебаний маятника не изменится, а центр качания будет располагаться в точке
О. То есть точки О и О1 обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки
О и О1 и сравнить эти формулы.
Рассмотрим пружинный маятник (или в общем случае так называемый
линейный гармонический осциллятор), то есть материальную точку массой
m, совершающую линейные гармонические колебания под действием упругой силы
F:
F = – k x (для пружины это – закон Гука).
Второй закон Ньютона для такого маятника запишется так:
,
или
Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:
Источник
Физическим маятником называется твердое тело, способное совершать
колебания вокруг неподвижной точки, не совпадающей с его центром инерции
Физическим маятником называется твердое тело, способное
совершать колебания вокруг неподвижной точки, не совпадающей с его центром
инерции. В положении равновесия центр инерции маятника С под точкой подвеса
маятника О, на одной с ней вертикали (рис. 170). При отклонении маятника от
положения равновесия на угол возникает вращательный момент,
стремящийся вернуть маятник в положение равновесия. Этот момент равен
(67.1) |
где m— масса
маятника» а l-расстояние между точкой подвеса и центром инерции маятника. Знак
«-» имеет то же значение, что и в случае формулы (66.1). Обозначив момент
инерции маятника относительно оси, проходящей через точку подвеса, буквой lможно написать:
(67.2) |
Рис.
170.
В случае малых колебаний (67.2) переходит в уже известное
нам уравнение:
(67.3) |
Через обозначена в данном случае следующая
величина:
(67.4) |
Из уравнений (67.3) и (67.4) следует, что при малых
отклонениях от положения равновесия физический маятник совершает гармонические
колебания, частота которых зависит от массы маятника, момента инерции маятника
относительно оси вращения и расстояния между осью вращения и центром инерции
маятника. В соответствии с (67.4) период колебания физического маятника
определяется выражением
(67.5) |
Из сопоставления формул (66.6) и (67.5) получается, что
математический маятник с длиной
(67.6) |
будет иметь такой период колебаний,
как и данный физический маятник. Величину (67.6) называют приведенной длиной
физического маятника. Таким образом, приведенная длина физического маятника —
это длина такого математического маятника, период колебаний которого совпадает
с периодом данного физического маятника
Точка на прямой, соединяющей точку подвеса с центром
инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром
качания физического маятника (см. точку О’ на рис.107).
По теореме Штейпера момент инерции маятника l может быть
представлен в виде
(67.7) |
где l0 — момент инерции
относительно оси, параллельной оси вращений и проходящей через центр инерции
маятника. Подставив (67.7) в формулу (67.6), получаем:
(67.8) |
Из (67.8) следует, что приведенная длина всегда больше 1,
так что точка подвеса и центр качания лежат по разные стороны от центра
инерции.
Подвесим маятник в точке, совпадающей с центром качания О’ В
соответствии с (67.8) приведенная длина в этом случае будет равна
(67.9) |
где l’ — расстояние между
первоначальным центром качания и центром инерции маятника. Учитывая, что , выражение (07.9)
можно записать следующим образом:
Выражение, стоящее в квадратных скобках, равно нулю.
Действительно, равно
I—моменту инерции относительно первоначальной оси
вращения; этой же величине в соответствии с (67.6) равно выражение mllпр. Таким образом, мы приходим к выводу,
что при подвешивании маятника в центре качания приведенная длина, а значит, и
период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и
центр качания обладают свойством взаимности при переносе точки подвеса в центр
качания прежняя точка подвеса .становится новым центром качания.
На установленном нами свойстве взаимности основано
определение ускорения силы тяжести с помощью так называемого оборотного
маятника. Оборотным называется такой маятник, у которого имеются две
параллельные друг другу, закрепленные вблизи его концов опорные призмы, за
которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и
закрепляться на нем тяжёлые грузы. Перемещением грузов добиваются того, чтобы
при подвешивании маятника за любую из призм период колебаний был одинаков.
Тогда расстояние между опорными ребрами призм будет равно lпр.
Измерив период колебаний маятника и зная l™, можно по Формуле
найти ускорение силы тяжести g.
Источник
Какой самый важный инструмент заядлого геймера? Мышка? Клавиатура? Продвинутый монитор с частотой обновления 144 Гц? Нет! Правильный ответ — игровое кресло.
А если без шуток, то выбор вашего личного «трона» — ответственное дело. Ведь максимальный комфорт и продолжительность игровой сессии напрямую зависят от того, насколько удобно вы в нем расположитесь.
А за эргономику девайса отвечают, прежде всего, ̶д̶и̶з̶а̶й̶н̶е̶р̶ы конструктивные особенности кресла, в том числе механизм качания. Спина и шея скажут большое спасибо за удобное положение, поддержку и опору. И наоборот — отплатят болью за выбор «неправильного» кресла. Давайте разберемся, как им угодить и какой выбор нужно сделать, чтобы комфортно играть длительное время. Начнем с истоков.
Пиастра
Пиастра — это не механизм качания, но упомянуть ее необходимо. Она — отправная точка для сравнения других механизмов. Представляет собой блок с рычагом для управления газлифтом. По нажатию рычага вверх кресло под тяжестью сидящего опускается вниз. Если снова потянуть рычаг, то сиденье вернется в изначальное положение (при отсутствии нагрузки на нем).
Пиастра — самый простой и, как следствие, дешевый механизм, который устанавливается на большинство бюджетных кресел.
Газлифт — сленговое название специальной блокируемой газовой пружины в офисных и игровых креслах. При закрытом клапане пружина очень жёсткая и под весом человека имеет короткий ход, подпружинивая кресло. При открытом клапане шток может перемещаться на полную длину пружины. Так регулируют кресло по высоте.
Пружинно-винтовой механизм
Как и пиастра, бюджетный вариант, позволяющий регулировать наклон спинки, ее высоту и расстояние от сиденья (не во всех моделях). А вот качаться на таком кресле не получится.
Перманент-контакт
С помощью механизма можно регулировать высоту и жесткость отклонения спинки, а также глубину посадки. В основе перманент-контакта упругая пружина, прижимающая спинку кресла к спине пользователя. Как и в предыдущем случае, такая конструкция качаться не позволит.
Топ-ган
Нет, это не название фильма или сетевого шутера. Это самый популярный механизм качания для офисных и игровых кресел. Его также называют центрированным механизмом качания или DMS. Ось такого механизма находится по центру кресла (отсюда и название). Угол наклона при качании в среднем составляет от 90 до 130 градусов.
Что умеет топ-ган:
- Опускает и поднимает сиденье с помощью рычага, воздействующего на газлифт. Пиастра в чистом виде.
- Включает или отключает механизм качания тем же рычагом (движением вправо-влево).
- Регулировочным винтом можно настраивать пружину, отвечающую за жесткость качания. Этот параметр определяют, исходя из веса пользователя. Чем вес больше, тем пружина должна быть жестче. И наоборот, для легких людей пружину следует ослабить.
Преимущества механизма DMS:
- Соотношение цена-качество. Топ-ган — это золотая середина между креслами без механизма качания и продвинутыми «качательными» моделями.
- Надежность. Данный механизм уступает более дорогим конкурентам по сроку службы. Но это не значит, что он сломается на следующий день. Большинство таких кресел спокойно выдерживает нагрузку от 90 до запредельных 180 кг.
Единственный серьезный минус топ-гана — при полном наклоне ноги сидящего отрываются от пола. Это усиливает нагрузку на позвоночник сидящего. К тому же кресло может запросто опрокинуться, если раскачиваться сверх меры.
Существует также усовершенствованная версия под названием мультитопган (топ-ган люкс или DMSL). Она отличается наличием второго рычага. С его помощью можно регулировать наклон спинки кресла.
Цена обычных топ-ганов начинается от 7 500 рублей. Мультитопганы стоят чуть дороже: от 9 500 рублей.
Во всех случаях указана среднерыночная стоимость. Всегда можно найти варианты как чуточку дешевле, так и кресла по цене хорошего игрового компьютера.
Deep Tilt
Deep Tilt — это механизм глубокого качания или коленный механизм. Имеет те же самые регулировки, что и топ-ган, и, в целом, очень похож на него. Визуально отличается наличием двух рычагов: один — для регулировки высоты, другой — для активации механизма качания. Deep Tilt превращает игровое кресло в почти настоящее кресло-качалку. В нашей стране распространения не получил, но интересные образцы найти все равно можно.
Мультиблок
Лучшее, что можно найти на рынке. Имеет те же преимущества, что и мультитопган, но дополнительно позволяет регулировать отклонение кресла во время качания и фиксировать спинку в пяти разных положениях. Отличается более продвинутой и плавной настройкой под каждого конкретного человека.
Мультиблоки бывают как центрированного типа, так и со смещенной осью. Последние гарантируют постоянный контакт ног сидящего с полом. Независимо от того, качаетесь ли вы или кресло находится в рабочем положении.
Цены на такие кресла начинаются от бюджетных 7 000 рублей, но есть и модели, которые стоят в 10 раз дороже.
Мультиблок с синхромеханизмом
Такой вариант позволяет синхронно изменять градус наклона спинки и сиденья. В стандартных креслах такого типа спинка изменяет наклон на 3-4 градуса, а сиденье синхронно — на 1 градус.
Преимущество механизма — регулировка нагрузки в зависимости от веса пользователя. Она обеспечивает максимально комфортные условия для позвоночника.
Стоимость таких кресел начинается от 12 000, продвинутые модели стоят чуть дороже — 15-20 тысяч рублей.
Мультиблок с асинхронным механизмом
В данном случае спинка и сиденье регулируются отдельно. Такое кресло можно подстроить под антропометрические особенности любого человека, особенно если вы обладаете нестандартными параметрами.
Общие преимущества мультиблоков:
- Самый высокий комфорт и эргономика среди конкурентов. Мультиблок максимально снизит нагрузку на позвоночник.
- Более высокая надежность и долгий срок службы.
- Чаще всего мультиблоки оснащены опцией «Антишок». Она гарантирует, что после снятия блокировки кресло не вернется резко в исходную позицию, тем самым ошарашив сидящего. Необходимо приложить некоторое усилие, чтобы вернуть его в рабочее положение.
Минусы вытекают из преимуществ. Во-первых, мультиблок — массивная тяжелая конструкция, для управления которой необходимо прикладывать больше усилий. Во-вторых, высокая стоимость механизма.
Заключение
Если вы киберспортсмен или просто геймер, проводящий много времени за игрой, имеет смысл купить мультиблок с синхромеханизмом. Выйдет дороже, но экономия на качественном игровом кресле в дальнейшем аукнется непредвиденными расходами на восстановление здоровья. Ну, а если бюджет совсем поджимает, то обратите внимание на мультитопганы. Они все еще гораздо лучше, чем самые простые игровые кресла без нужных регулировок.
Источник